yourdomain.com

После разделения "Математики" не знаю, куда помещать тему, пока кидаю сюда.

Возникла вот какая задача. Есть функция f(x) на отрезке -1<x<1, зависящая от бесконечного набора параметров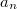 $$a_n$$

$\displaystyle f(x)=1+\sum_{k=1}^\infty(4k+1)a_{2k}P_{2k}(x),$

где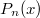 $$P_n(x)$$

--- полиномы Лежандра. Есть условие, что функция должна быть положительна на отрезке -1<x<1. В пространстве параметров это условие задает некую область допустимых значений. Интересует проекция этой области на плоскость $$(a_2,a_4)$$

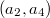. Можно ли ее как-то в явном виде вычислить?

P. S. Для тех, кого интересует физика

. f --- функция распределения ориентации кристалликов в поликристаллической среде, в рассматриваемой модели зависит только от одного из углов Эйлера. $$a_2$$

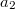и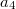

--- те моменты функции распределения, от которых зависит усредненный тензор Гука поликристаллической среды. Функция распределения толком не известна, интересует, существуют ли общие ограничения на усредненный тензор Гука и каковы они.

посмотрела сейчас определения полиномов Лежандра...
полиномы Лежандра с чётными номерами - чётные функции, можно рассматривать от 0 до 1

вначале надо определять область сходимости ряда, разве нет?
у степенных рядов это признаком Даламбера обычно делают, а у вас эти неизвестные параметры...

Со сходимостью все как раз просто: полиномы Лежандра составляют полную ортогональную систему функций на -1<x<1.

1. Критерий сходимости ряда по ортогональной системе $\sum (4k+1)^2a_{2k}^2||P_{2k}^2||=2\sum (4k+1)a_{2k}^2<\infty$
2.Пусть он сходится к функции f, тогда $a_{2k}=\frac 12\int_{-1}^1P_{2k}(x)f(x)dx$
3.Проекция области $$(f>0)$$

на плоскость $$<a_2,a_4>$$

- это множество таких пар $$(a_2,a_4)$$

для которых существует положительная f, что а) соотношения из пункта 2 выполняются для k=0 ( $$a_0=1$$

?)б)соотношения из пункта 2 выполняются для k=1 и 2, в)существуют такие $$a_6,a_8,...$$

что эти соотношения выполняются и для них, а ряд (1) сходится. Но раз речь о Лежандрах, то в) автоматом идет из а) и б).Предположим, нашли положительную f, что а) и б). Не доказываю, но можно сделать, что f Липшицева и даже гладкая.Определим коэффициенты формулами (2) и по неравенству Бесселя ряд (1) сходится.
4."Усеченная проблема моментов": При каких $$f_2,f_4$$

существует положительная мера $d\mu$ такая, что $\displaystyle \\1=\int_{-1}^1d\mu\\f_2=\int_{-1}^1x^2d\mu\\f_4=\int_{-1}^1x^4d\mu$
Я не помню на память, ответ вроде такой:
$\displaystyle \\f_4<f_2<1\\1-2f_2+f_4>0$
задает тупоугольный треугольник Т на плоскости $$f_4$$

5. Из $\\a_2=\frac 14(3f_2-1)\\a_4=\frac 1{16}(35f_4-30f_2+3)$ $ искомая проекция получается из треугольника Т линейным преобразованием

Слишком лихо Ладно, расскажу свои мысли.

Первая мысль такая: будем полагать $a_{2k}=0$ при $$k>n$$

. Тогда функция распределения --- многочлен конечной степени. Как-нибудь определим область допустимых параметров. Понятно, что для бОльшего $$n$$

она может только расшириться. Будем надеяться, что существует предел

"Как-нибудь" удается проделать, хотя не без геморроя, для случая, когда только $$a_2$$

и

отличны от нуля. Ответ такой: область допустимых параметров --- внутренность эллипса $a_4-\frac5{14}a_2^2+\frac57a_2a_4-\frac{27}7a_4^2=0$ , а также внутренность (криволинейного) треугольника, образованного эллипсом и касательными $1-\frac52a_2+\frac{27}8a_4=0$ , $$1+5a_2+9a_4=0$$

к нему. Так что ваш ответ с треугольником вряд ли верный.

Вторая мысль более геометрическая: рассмотрим $$x$$

как параметр, тогда равенство $$f=0$$

задает семейство гиперплоскостей в пространстве $(a_2,a_4,\ldots)$ . Это семейство, наверное, имеет огибающую. Вот проекцию этой огибающей на плоскость $$(a_2,a_4)$$

надо найти. Можно, например, брать конечное число параметров и конечное число точек по $$x$$

. Тогда гиперплоскости высекут многогранник. Его проекция --- ломаная, а найти ее, наверное, можно методами, развитыми в математическом программировании. Но мне тут не хватает знаний и воображения.

P. S. По поводу ограниченности области. С одной стороны, компоненты усредненного тензора Гука не могут превосходить максимальной компоненты исходного тензора. С другой --- компоненты усредненного тензора Гука являются линейными функциями $$a_2$$

и

. Расчет показывает, что разные компоненты растут по разным направлениям в плоскости $$(a_2,a_4)$$

. Поэтому с большой вероятностью область допустимых параметров ограничена. Надо мне будет вычислить границы, исходя из этих соображений...

Маленькая поправочка к предыдущему сообщению: компоненты усредненного тензора не могут быть больше максимальной компоненты исходного, умноженной на 9

Решил задачу по наводке Ian'а, за что ему спасибо. Итак, имеется функция распределения f(x) на -1<x<1. Тогда для моментов второго и четвертого порядков выполняются неравенства $\displaystyle 0<M_2^2<M_4<M_2<1.$

Теперь достаточно доказать обратное, то есть что возможно построить функцию распределения, если моменты удовлетворяют этим неравенствам, и область допустимых значений моментов у нас в кармане. Нетрудно проверить, что функция

$\displaystyle f(x)=\frac{M_4-M_2^2}{M_2}\delta(x)+\frac{M_2-M_4}{M_2(1-M_2)}\delta\bigl(x-\sqrt{M_2}\,\bigr)+\frac{M_4-M_2^2}{1-M_2}\delta(x-1)$

(все коэффициенты положительны!) имеет моменты $$M_2$$

и

. Остается пересчитать моменты в мои параметры $$a_2$$

и

.

P. S. Функцию распределения можно написать много проще

$\displaystyle f(x)=\frac{M_4-M_2^2}{M_4}\delta(x)+\frac{M_2^2}{M_4}\delta\bigl(x-\sqrt{M_4/M_2}\,\bigr).$

peregoudov писал(а):Source of the post $\displaystyle M_2^2<M_4$

Да, это неравенство Гельдера, и оно сильнее чем $2M_2-1\leqslant M_4$ .Давно решал, забыл.
Удивительно, что все решенные усеченные проблемы моментов(ПМ) не сведены в одной книге, в которой можно посмотреть решения и сослаться. Например, решение ПМ для $$M_0=1,M_1,M_2,M_3$$

эквивалентно UVW-теореме, доказанной сравнительно недавно.

Окончательные уравнения границы в терминах $$a_2$$

и

$\displaystyle 12a_4<5a_2+7,\quad 18a_4>35a_2^2-10a_2-7.$

Итак, окончательная картинка. Красным показана новая граница области, черным --- старая граница.

И еще я теперь знаю, куда нужно перенести тему: в Теорию вероятностей.

Так, теперь меня интересует обобщение этой задачи. Пусть функция распределения

$\displaystyle f(\theta,\phi)=1+\sum_{l=1}^\infty\sum_{m=-l}^l(2l+1)a^m_lP^m_l(\cos\theta)e^{im\phi},$

где $$P^m_l(x)$$

--- присоединенные функции Лежандра. Нужно определить границы для $$a^m_2$$

,

.

Эта задача выела мне мозг!

Но сначала уточнения к постановке. Как и в одномерном случае, симметрия приводит к тому, что интересны только коэффициенты $a^{0,2}_2$ и $a^{0,2,4}_4$ , то есть всего пять штук. Они являются средними функций (с учетом нормировки)

$\displaystyle \tfrac12(1-3\cos^2\theta),\quad -\sqrt{\tfrac38}\,\sin^2\theta\,e^{2i\phi},\quad \tfrac18(35\cos^4\theta-30\cos^2\theta+1),$
$\displaystyle \sqrt{\tfrac5{32}}\,\sin^2\theta\,(7\cos^2\theta-1)e^{2i\phi},\quad \sqrt{\tfrac{35}{128}}\,\sin^4\theta\,e^{4i\phi},$

или, обозначая $x=\cos^2\theta$ , $y=\sin^2\theta\cos^2\phi$ (от $e^{im\phi}$ в силу симметрии задачи остается только вещественная часть), уже без учета нормировки и взяв простейшие комбинации, средними от

$\displaystyle x,\quad y,\quad x^2,\quad xy,\quad y^2.$

При этом $0\leq x\leq1$ , $0\leq y\leq1$ .

Итак, задача может быть переформулирована в виде "двумерной усеченной проблемы моментов": при каких $f_1,\ldots,f_5$ существует мера на квадрате $0\leq x\leq1$ , $0\leq y\leq1$ , такая что

$\displaystyle f_1=\overline x,\quad f_2=\overline y,\quad f_3=\overline{x^2},\quad f_4=\overline{xy},\quad f_5=\overline{y^2}.$

Мне показалось удобнее оперировать с центральными моментами

$\displaystyle Dx=\overline{(x-\overline x)^2},\quad Dy=\overline{(y-\overline y)^2},\quad K=\overline{(x-\overline x)(y-\overline y)}.$

Насколько я понимаю, основные условия на них --- условия положительной определенности ковариационной матрицы

$\displaystyle 0\leq Dx,\quad 0\leq Dy,\quad K^2\leq Dx\,Dy.$

Есть еще ограничения сверху на дисперсии, следующие из $\overline{x^2}\leq\overline x$ , $\overline{y^2}\leq\overline y$

$\displaystyle Dx\leq\overline x(1-\overline x),\quad Dy\leq\overline y(1-\overline y).$

Наконец, есть условия на средние

$\displaystyle 0\leq\overline x\leq1,\quad 0\leq\overline y\leq1.$

Естественно, пытался использовать тот же прием, что в одномерном случае: явно подобрать функцию распределения в виде линейной комбинации дельта-функций. Но задача какая-то заколдованная! Уж столько вариантов перебрал, никак не могу добиться, чтобы все коэффициенты были положительны :blink:

P. S. Я, конечно, неправильно область написал: там не квадрат, а треугольник $0\leq x\leq1$ , $0\leq y\leq1-x$ , поскольку $x+y=\cos^2\theta+\sin^2\theta\cos^2\phi\leq1$ .

yourdomain.com

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров

Область допустимых значений параметров