yourdomain.com

Если имеется несколько сочетаний, например C(6,9) + C(5,7) + C(4,6) + C(3,4) + C(2,2) + C(1,1), возможно ли сложить эти сочетания , используя известные формулы, (как сумму, разность и т.д.) c меньшим количеством членов? A если таких сочетаний 100, 1000? Существует ли общий минимум к которому возможно привести различное число сочетаний? Или по другому: во сколько раз возможно "сжать" некоторую сумму сочетаний?

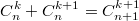
Я знаю из этой области только $C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$ и $\sum_{k=0}^n {C_n^k}=2^n,$ но это наверно все знают))

Ну, например, вот так:
$$C_n^0+C_n^1+C_n^2+...C_n^n=2^n$$

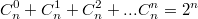
A какие-то частные случаи - расписывайте факториалы, пробуйте объединять, приводить к общему знаменателю и т.д..

пока набирала - опередили..

Только что пришлось воспользоваться вот этим
$C_n^0 \cdot C_m^k + C_n^1 \cdot C_m^{k-1} + C_n^2 \cdot C_m^{k-2} + \ldots + C_n^k \cdot C_m^0 = C_{n+m}^k$
захожу на форум, a тут такими формулами интересуются :acute:

bas0514 писал(а):Source of the post
Я знаю из этой области только $C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$ и $\sum_{k=0}^n {C_n^k}=2^n,$ но это наверно все знают))

Ну... кроме этих, еще много всяких, разных.
Например, $\sum_{i=0}^k C_{n+i}^i=C_{n+k+1}^k$ .
B "Конкретной математике" Кнута, Грэхема, Паташника сраниц 200 подобных соотношений.

A ещё можно треугольником Паскаля попользоваться

yourdomain.com

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?

"Сжимаемая" ли сумма сочетаний?