yourdomain.com

не знаю
мне, наверно, надо 1 том почитать

Swetlana писал(а):Source of the post
не знаю
мне, наверно, надо 1 том почитать

Вы свято верите в то, что 1 том содержит все ответы?

Спокойно, не переходя на личности, начинаем рассуждать. Выборка воспроизводит распределение? Среднее по выборке характеризует центр распределения? Дисперсия выборки характеризует "ширину" распределения? Как - это вопрос третьего порядка.

вообще-то я всего лишь хотела стать приятным собедником

вот все мои рассуждения
что дано
1. случайная величина непрерывна, но принимает лишь счётное число значений (иначе была бы не сумма, а интеграл)
2. вероятность принятия значения x_n равна 1/n (иначе какая была бы связь между матожиданием и предложенной суммой)
3. матожидание - ряд с общим членом x_n/n не является абсолютно сходящимся
4. то же для дисперсии
...

что нужно доказать (или построить контрпример) пока не поняла
пожалуй, стОит почитать первый том

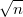
По теореме Колмогорова выборочная оценка равномерно сходится к функции распределения со скоростью . Следовательно увеличение объема выборки улучшит оценку.

sw_pro@mail.ru писал(а):Source of the post
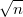
По теореме Колмогорова выборочная оценка равномерно сходится к функции распределения со скоростью . Следовательно увеличение объема выборки улучшит оценку.

К чему будет сходиться среднее выборочное для указанного распределения?
К чему будет сходиться выборочная оценка дисперсии для указанного распределения?

Swetlana писал(а):Source of the post
вообще-то я всего лишь хотела стать приятным собедником

Светлана, спасибо! Я могу только надеяться, что Вы предварительно посмотрели, во что сознательно вляпались!

Andrew58 писал(а):Source of the post К чему будет сходиться среднее выборочное для указанного распределения?
К чему будет сходиться выборочная оценка дисперсии для указанного распределения?

Если речь о распределении указанном в посте #1, то ни к чему. Поскольку распределение СВ моментов не имеет. Если речь о посте #37, то распределение СВ не известно, и нельзя заранее сказать, к чему будут сходится оценки первого и второго моментов.

sw_pro@mail.ru писал(а):Source of the post
Если речь о посте #37, то распределение СВ не известно, и нельзя заранее сказать, к чему будут сходится оценки первого и второго моментов.

Браво!!! Если распределение заранее не известно - нефига его выборками нащупывать!!!

Andrew58 писал(а):Source of the post Браво!!! Если распределение заранее не известно - нефига его выборками нащупывать!!!

Отчего-же. Выборка дает возможность оценить функцию распределения СВ. А вот, будет ли это распределение иметь моменты, зависит от вида функции. И вообще задача из #1 к ТВ и МС отношения не имеет. Это из анализа. Если интеграл расходится, то из этого следует отсутствие равномерной сходимости для соотв. ряда. Т.е. возможны случаи, когда ряд сойдется. Но в этом случае сумма ряда не будет иметь никакого отношения к моментам.

Андрей, посмотрела вчера, а осознала только сегодня
сумма гармонического ряда не равна 1, так что всё написанное мною выше бред
если у величины несчётное число значений, то это действительно выборка, а третьего тома у Феллера нет

Andrew58 писал(а):Source of the post
У меня есть выборка объемом N - это экспериментальные данные, и с ними уже ничего не поделаешь. У меня есть подозрение (и кое-какие соображения), что измеряемая величина была распределена по закону
.
Я хотел бы увеличить объем выборки, если это дает мне возможность точнее определить параметры распределения, а дает ли?

Однозначно даст. Чем больше выборка, тем лучше она характеризует генеральную совокупность. А параметры сдвига и масштаба можно оценить и по выборочным квартилям.