Область допустимых значений параметров

Ian · Сообщение **Ian** » 23 ноя 2012, 06:58

Преобразование
$\displaystyle \\\tilde x=1-x-y\\\tilde y=x$ переводит треугольник, носитель меры, на себя, всего их 6 таких, включая тождественное и неинтересное меняющее местами х и у
Ему соответствует линейное преобразование
$\tilde f_3=\iint(1-x-y)^2d\mu=1+f_3+f_5-2f_4-2f_1-2f_2$
и аналогично для всех компонент вектора $$(1,f_1,f_2,..f_5)$$

Получилось линейное преобразование, переводящее искомую область на себя.
Чем это поможет, не знаю

peregoudov · Сообщение **peregoudov** » 23 ноя 2012, 11:18

Я тут почитал литературу, конкретно

Математическую энциклопедию, статья "Моментов проблема"
Ахиезер "Класическая проблема моментов и некоторые вопросы анализа, связанные с нею"
Крейн, Нудельман "Проблема моментов Маркова и экстремальные задачи"

К сожалению, математики все больше жуют одномерный случай. Явного решения моей задачи нигде не нашел. По идеологии ближе всего Крейн, там рассматривается усеченная проблема, правда, только в одномерном случае. Но, возможно, удастся разобраться и применить идеи к двумерному случаю.

В энциклопедии и у Ахиезера рассматривается только полная проблема моментов и не для треугольника, а для квадрата (ну, это можно преобразовать). Трудность в том, что условие разрешимости довольно запутанное и непонятно, как из него получить условия только на низшие моменты, оставляя высшие произвольными. Например, в одномерном случае условие разрешимости можно записать в символическом виде

$\displaystyle \overline{x^k(1-x)^p}\geq0,\quad k,p=0,1,2,\ldots$

Во-первых, все условия линейные по моментам, а нужно квадратичное условие $\overline{x^2}\geq\overline x^2$ . Во-вторых, $\overline x$ и $\overline{x^2}$ входят во все условия с $$k=0,1,2$$

.

peregoudov · Сообщение **peregoudov** » 26 ноя 2012, 13:16

Опишу промежуточный этап своих поисков.

Есть одна хорошая новость: я почти все, что есть в литературе, придумал сам Не смог придумать только одной очень важной вещи, которая позволяет свести задачу функционального анализа к конечномерной. Вот о ней в первую очередь и расскажу. Прошу ногами не пинать, буду рассказывать как физик, на уровне идей, не заморачиваясь особо математической строгостью.

Первый шаг --- перейти от задачи по поиску меры на треугольнике к эквивалентному поиску положительного линейного функционала $\Phi[f(x,y)]$ на непрерывных функциях в треугольнике. Положительного в том смысле, что если $$f(x,y)>0$$

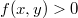
$\forall x,y$ из треугольника, то $\Phi[f(x,y)]>0$ . Понятно, что проверять положительность для всех функций --- хлопотное дело. К счастью, существует теорема Рисса о продолжении, которая гарантирует, что функционал, заданный на подпространстве, можно расширить до функционала во всем пространстве. Для нас это означает, что можно ограничиться подпространством многочленов не выше второй степени, $$p_2(x,y)=c_0+c_1x+c_2y+c_3x^2+c_4xy+c_5y^2$$

. Поскольку мы хотим, чтобы средние были равны $$f_k$$

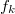
, значение функционала на этих функциях очевидно из его линейности $\Phi[p_2(x,y)]=\sum_k c_kf_k$ . Для положительных на треугольнике многочленов значение функционала должно быть положительным: если $$c_0+c_1x+c_2y+c_3x^2+c_4xy+c_5y^2>0$$

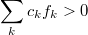
на треугольнике, то $\sum_kc_kf_k>0$ . Описать область $$f_k$$

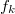
--- вот задача, которую надо решить.

Теперь я расскажу о двух способах решения этой задачи, в основном следуя Крейну и Нудельману. Первый способ по сути дела совпадает с предложенным мной в пятом сообщении построением огибающей. Нетрудно видеть, что множество положительных функций представляет собой выпуклый конус: вместе с функкцией $$f(x,y)$$

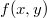
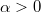
ему принадлежит луч $\alpha f(x,y)$ , $\alpha>0$ , а вместе с функциями $$f_1(x,y)$$

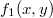
и

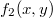
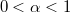
--- соединяющий их отрезок $\alpha f_1(x,y)+(1-\alpha)f_2(x,y)$ , $0<\alpha<1$ . Образующие этого конуса --- лучи тех положительных функций, которые не могут быть представлены как сумма двух других положительных функций.

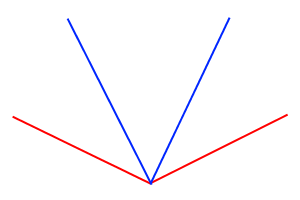
Если вектор ${\bf c}$ лежит в конусе, то вектор ${\bf f}$ , определяемый неравенством ${\bf cf}>0$ лежит в дуальном конусе, образующие которого направлены вдоль нормалей к поверхности исходного конуса.

Соотношение дуальности аналогично преобразованию Лежандра или касательному преобразованию: дульный к дуальному конус совпадает с исходным. Таким образом, для определения области допустимых моментов достаточно найти конус (так называемую коническую оболочку), в котором лежит двумерная поверхность, заметаемая вектором ${\bf p}=(1,x,y,x^2,xy,y^2)$ при изменении $$x,y$$

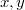
в треугольнике.

К стыду своему должен сказать, что задача эта, вроде бы и не столь уж многомерная (можно еще выкинуть первую, постоянную, компоненту вектора и искать сечение конуса --- выпуклую линейную оболочку), оказалась мне пока не под силу

Второй способ решения задачи состоит в использовании удобного представления для положительных многочленов. Например, в одномерном случае есть теорема (многим она, наверняка, известна), что положительный на всей оси многочлен $$p(x)$$

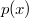
(по необходимости четной степени) представлется в виде суммы квадратов двух других многочленов $$p(x)=a^2(x)+b^2(x)$$

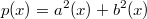
. Есть обобщение этой теоремы для отрезка [0,1]: многочлены четной степени могут быть представлены в виде $$p(x)=a^2(x)+x(1-x)b^2(x)$$

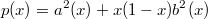
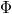
. Подстановка этого представления в условие положительности функционала $\Phi$ немедленно приводит к условию положительности квадратичных форм

$\displaystyle \overline{x^{p+q}}a_pa_q+\overline{x^{1+p+q}(1-x)}b_pb_q>0$

( $$a_p$$

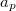
и

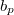
--- коэффициенты многочленов $$a(x)$$

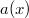
и

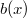
), которое, в свою очередь, немедленно дает условия на моменты.

К сожалению, подобной теоремы для многомерного случая нет и быть не может. Один из первых явных примеров --- многочлен Моцкина (Motzkin) $$x^2y^2(x^2+y^2-3)+1$$

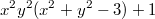
. Положительный многочлен от двух переменных может быть представлен в виде суммы четырех квадратов рациональных функций, но это не то, что нам нужно.

Среди результатов, имеющих отношение к задаче, есть теорема Гендельмана (Handleman), которая утверждает, что положительный многочлен можно представить в виде суммы одночленов по функциям, задающим границу области (у нас это $$x$$

,

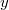
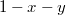
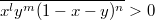
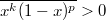
) с положительными коэффициентами. Это приводит к условиям $\overline{x^ly^m(1-x-y)^n}>0$ , с которыми, как и с условиями $\overline{x^k(1-x)^p}>0$ в одномерном случае, непонятно что делать :huh:

В конце концов у нас многочлен второй степени, линии уровня которого --- кривые второго порядка. Тут нам светит полная ветвлений задача о касании эллипса/гиперболы/параболы с треугольником

peregoudov · Сообщение **peregoudov** » 26 ноя 2012, 15:22

Хочу рассказать еще об одном подходе, навеянном одномерной задачей. Буду пользоваться механической терминологией и рассуждать нестрого. Попытаемся заменить произвольное распределение масс по треугольнику на распределение, когда массы сосредоточены в конечном числе точек, так чтобы моменты до второго порядка включительно оставались неизменными. Рассуждая физически, начнем со случая, когда масса уже сосредоточена в конечном, но большом числе точек, и посмотрим, нельзя ли это число уменьшить. А потом будем наивно считать, что результат, справедливый для конечного числа точек, остается справедливым и для произвольного распределения массы.

Опыт одномерного случая учит нас, что любое распределение массы на отрезке можно заменить двумя точками, одна из которых лежит в заданном конце отрезка. Из этого наблюдения проистекает замечательная теоремка: систему двух точек можно заменить эквивалентной системой двух точек, расположенных на той же прямой, причем одна из новых точек лежит в заданной точке прямой вне исходного отрезка (а вторая --- внутри. Или наоборот: внутри положение задано, а вовне определяется).

С помощью этого нехитрого приема можно все точки изнутри треугольника, кроме одной, вынести на границы

Те же рассуждения для стороны треугольника позволяют все вынести в заданный угол, кроме одной точки. Если я не ошибся нигде с особыми случаями (обычная головная боль математиков

), то любое распределение масс сводится к такому: одна точка в заданной вершине треугольника, еще две на прилегающих сторонах, и еще одна внутри. В частных случаях "сторонние" точки могут вылезать в углы, а "внутренняя" --- ложиться на сторону. Некоторые массы в частных случаях могут равняться нулю.

Если внутренняя точка лежит вне треугольника, образованного остальными тремя, то уменьшить количество точек описанным выше приемом уже нельзя. Хотя остается неясно, нельзя ли и в этом случае заменить четыре точки на три.

Ограничения на параметры точек известны: массы неотрицательны, а точки лежат в треугольнике. Обращая зависимость моментов от параметров точек, получаем условия на моменты. К сожалению, так просто обратить нельзя: параметров 7, а моментов 5. Так что в действительности получается условие разрешимости системы неравенств для двух каких-то параметров, например, координат внутренней точки. При таком выборе свободных параметров почти все неравенства сводятся к линейным

$\displaystyle \begin{gathered} 0<x,\quad 0<y,\quad x+y<1,\\ 0<\overline{x^2}\,y-\overline{xy}\,x<\overline{x}\,y-\overline{xy},\\ 0<\overline{y^2}\,x-\overline{xy}\,y<\overline{y}\,x-\overline{xy} \end{gathered}$

и только одно выглядит запутанным

$\displaystyle (xy-\overline{xy})-\frac{x(\overline{x}\,y-\overline{xy})^2}{\overline{x^2}\,y-\overline{xy}\,x}-\frac{y(\overline{y}\,x-\overline{xy})^2}{\overline{y^2}\,x-\overline{xy}\,y}>0.$

Ian · Сообщение **Ian** » 27 ноя 2012, 06:18

peregoudov писал(а):Source of the post
Соотношение дуальности аналогично преобразованию Лежандра или касательному преобразованию: дуальный к дуальному конус совпадает с исходным.

Не всегда. Есть вырожденные случаи которые именно тут и сбываются. Дуальный конус в 6-мерном пространстве к конусу размерности меньше 6 $(k,ku,kv,ku^2,kuv,kv^2),k>0,u,v\geqslant 0,u+v\leqslant 1$ будет 6-мерным полупространством, дуальный же к полупространству -одномерный луч.То есть мы теряем информацию о том, каков был исходный конус:(

peregoudov · Сообщение **peregoudov** » 27 ноя 2012, 21:50

Вы не поняли. Там конус получается вполне себе шестимерный. В многомерном пространстве это трудно представить, рассмотрите трехмерное и выпуклую коническую оболочку векторов $$(1,x,x^2)$$

,

.

peregoudov · Сообщение **peregoudov** » 30 ноя 2012, 22:14

Все, я решил свою задачу. "Запутанное" условие оказалось не таким уж сложным. Чтобы пояснить решение, дадим геометрическую интерпретацию выписанных неравенств.

Линейные неравенства

$\displaystyle \begin{gathered} 0<\overline{x^2}\,y-\overline{xy}\,x<\overline{x}\,y-\overline{xy},\\ 0<\overline{y^2}\,x-\overline{xy}\,y<\overline{y}\,x-\overline{xy} \end{gathered}$

задают область лежащую ниже прямой BD и выше остальных прямых. Важно, что либо точка A, либо точка B (или обе сразу) лежат на границе допустимой области. Именно, A лежит на границе при выполнении условия

$\displaystyle \overline y\,\overline{x^2}-\overline x\,\overline{xy}>\overline{x^2}\,\overline{y^2}-\overline{xy}^2.$

Условие для B получается заменой $x\leftrightarrow y$ .

Ключом к решению является поведение функции

$\displaystyle \begin{aligned} &\Phi(x,y)={}\\ &\quad{}=\left[(xy-\overline{xy})-\frac{x(\overline{x}\,y-\overline{xy})^2}{\overline{x^2}\,y-\overline{xy}\,x}-\frac{y(\overline{y}\,x-\overline{xy})^2}{\overline{y^2}\,x-\overline{xy}\,y}\right](\overline{y^2}\,x-\overline{xy}\,y)(\overline{x^2}\,y-\overline{xy}\,x) \end{aligned}$

входящей в "запутанное" условие в окрестности точек A

$\displaystyle \Phi(x,y)=\frac{\overline{x^2}\,\overline{xy}(DxDy-K^2)}{\overline x^3}(\overline{x^2}\,y-\overline{xy}\,x)+\ldots$

и B (получается заменой $x\leftrightarrow y$ ). Здесь $Dx=\overline{x^2}-\overline x^2$ , $Dy=\overline{y^2}-\overline y^2$ , $K=\overline{xy}-\overline x\,\overline y$ --- центральные моменты, компоненты ковариационной матрицы.

Таким образом, в окрестности точек A или B в допустимой обрасти "запутанное" условие выполняется автоматически. В качестве решения системы неравенств можно выбирать точку A или B. При этом одна из четырех масс оказывается равной нулю. Например, при

$\displaystyle \overline y\,\overline{x^2}-\overline x\,\overline{xy}>\overline{x^2}\,\overline{y^2}-\overline{xy}^2$

выбираем точку A, тогда

$\displaystyle \begin{gathered} x_1=0,\quad y_1=0,\quad m_1=\frac{DxDy-K^2}{\overline{x^2}\,\overline{y^2}-\overline{xy}^2},\\ x_2=0,\quad y_2=\frac{\overline{x^2}\,\overline{y^2}-\overline{xy}^2}{\overline y\,\overline{x^2}-\overline x\,\overline{xy}},\quad m_2=\frac{(\overline y\,\overline{x^2}-\overline x\,\overline{xy})^2}{\overline{x^2}(\overline{x^2}\,\overline{y^2}-\overline{xy}^2)},\\ x_3=\frac{\overline{x^2}}{\overline x},\quad y_3=\frac{\overline{xy}}{\overline x},\quad m_3=\frac{\overline x^2}{\overline{x^2}}. \end{gathered}$

Если я нигде не ошибся с выявлением более слабых неравенств, то окончательные условия на моменты получаются такими

$\displaystyle \begin{gathered} \overline{xy}>0,\quad Dx>0,\quad Dy>0,\\ \overline x>\overline{x^2}+\overline{xy},\quad \overline y>\overline{y^2}+\overline{xy},\\ DxDy-K^2>0. \end{gathered}$

Попутно мы получили ответ на вопрос о представлении: твердое тело в виде треугольника с произвольным распределением масс может быть эквивалентно представлено тремя материальными точками, одна из которых лежит в заданной вершине, вторая --- на одной из сторон, прилегающих к этой вершине (на какой --- зависит от исходного распределения масс, иногда может быть, что на любой), а третья --- внутри треугольника.

yourdomain.com