Страница 1 из 2
Предел функции двух переменных
Добавлено: 24 июн 2015, 05:20
Mihail-Nor
Здравствуйте!
Пусть

и

- рациональные числа с нечётными числителями и знаменателями. Как можно доказать или опровергнуть, что


?
Предел функции двух переменных
Добавлено: 24 июн 2015, 17:50
vidok
a=1, b=1 дробь=1, a=0, b=0 дробь = 2/(x+y); x и y можно выбрать такими, чтобы дробь стала меньше чем эпсилон, для любого эпсилон > 0
Предел функции двух переменных
Добавлено: 24 июн 2015, 21:07
Mihail-Nor
Такие варианты

и

не рассматриваются, заданы некоторые
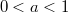
и
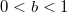
. Например,
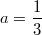
,
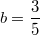
.
Предел функции двух переменных
Добавлено: 24 июн 2015, 21:49
Ian
Утверждение верно. На любой окружности радиуса R максимум дроби достигается при той переменной равной 0, у которой меньше показатель, а другая =+-R разумеется.Находим значение этого максимума ,типа R^{a-1} и видим что оно стремится к 0 при R к бесконечности
И надо заметить, что все тут определено и при отрицательных х,у в том смысле, что сначала х,у возводятся в четные степени числителя показателя степени, а потом уже извлекается корень нечетной степени, проще говоря, все, какие тут есть степенные функции, принимают только положительные значения.Но то, что степенные функции определены именно так, надо оговаривать. Не проще ли чтоб не будить ненужные философские рассуждения в некоторых людях,. как "х", так и "у" в условии писать везде по модулю
Предел функции двух переменных
Добавлено: 24 июн 2015, 22:17
Mihail-Nor
"На любой окружности радиуса R максимум дроби достигается при той переменной равной 0, у которой меньше показатель, а другая =+-R" - это неверно, вот пример графика этой дроби при

,

и

как в моём предыдущем сообщении,
![$$x \in [0, R]$$ $$x \in [0, R]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24x%20%5Cin%20%5B0%2C%20R%5D%24%24)
,

.
Да, такие степени определены при любых основаниях из-за чётного числителя всех показателей, а вся дробь определена и является положительным числом для любых

, если только

. Причём достаточно рассматривать первую четверть

,

- в остальных случаях значения дроби те же.

Предел функции двух переменных
Добавлено: 25 июн 2015, 06:41
vidok
Любые а и b не подойдут (при 1 например - неверно утверждение). А вобщем утверждение верно при некоторых a и b (интересно кстати определить при каких a и b в общем случае), что и написал
Предел функции двух переменных
Добавлено: 25 июн 2015, 08:33
Ian
Mihail-Nor, действительно это я не угадал, а построил - такой же график вышел
Ну раз оптимум при определенной (только от a,b зависящей) пропорции между х и у, гарантированно сработает неравенство Гельдера, в общем (для нашей задачи) виде это
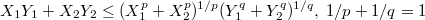
,либо оно же доставит контрпример
Теперь подставим
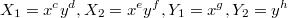
и подберем параметры c,d,e,f,g,h,p,q так, чтоб одна скобка обратилась в числитель, другая в знаменатель (с точностью до общего множителя у, который должен сократиться), третья в сумму квадратов
Пи-теорему не случалось применять? Веселое занятие, не хочу лишать удовольствия)
Предел функции двух переменных
Добавлено: 25 июн 2015, 13:40
Mihail-Nor
Что именно в выражении

нужно обратить во что?
Выражения

и

ведь не могут превратиться ни в числитель, ни в знаменатель исходной дроби - мешают не равные единице показатели
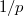
и
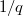
.
Предел функции двух переменных
Добавлено: 25 июн 2015, 13:52
12d3
А почему бы не попробовать предельно топорный метод: найти максимум функции на окружности и посмотреть, к чему этот максимум стремится при стремлении радиуса к бесконечности.
Предел функции двух переменных
Добавлено: 25 июн 2015, 13:57
Mihail-Nor
Хотелось бы как-то оценить сверху эту функцию на произвольной окружности. Не понятно, как это можно сделать.
Поиск точного максимума (приравнивание производной к нулю) приводит к очень сложному уравнению. Не понятно, как можно его решить.
 и
и  - рациональные числа с нечётными числителями и знаменателями. Как можно доказать или опровергнуть, что
- рациональные числа с нечётными числителями и знаменателями. Как можно доказать или опровергнуть, что

