И снова ряд Тейлора - полная энергия
Добавлено: 16 окт 2014, 18:32
Есть функция:
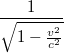
Надо разложить ее в ряд Тейлора при v_0=0. Получается:

Если вычислять производную при заданном v_0=0, то получается, что все выражение обращается в ноль, и остается только единица. То же самое происходит и с остальными членами, высшего порядка. Что я сделал неправильно? Ведь так не может быть - этот прием использовался для получения полной энергии релятивистской частицы, а там выражение-то известно, и я не понимаю, каким образом оно получается.
P.S. Не знал точно, в какой раздел поместить тему - вроде как физика, но вопрос чисто математического характера.
Надо разложить ее в ряд Тейлора при v_0=0. Получается:
Если вычислять производную при заданном v_0=0, то получается, что все выражение обращается в ноль, и остается только единица. То же самое происходит и с остальными членами, высшего порядка. Что я сделал неправильно? Ведь так не может быть - этот прием использовался для получения полной энергии релятивистской частицы, а там выражение-то известно, и я не понимаю, каким образом оно получается.
P.S. Не знал точно, в какой раздел поместить тему - вроде как физика, но вопрос чисто математического характера.