Страница 1 из 2
Найти точку на сфере
Добавлено: 21 окт 2013, 12:55
San1990
Добрый день форумчане!
Есть такая задачка. Даны три точки на сфере

. Где

- разница во времени прихода сигнала к і точки от времени прихода сигнала к первой. Тоесть когда появился сигнал мы не знаем. Но разницу между приходами сигнала к точкам мы знаем. (t3=>t2=>t1) Сфера единичная. Скорость распространения сигнала единичная. Нужно найти координаты точки от который был сигнал.
Что мне нужно: Идеи как это начать или литература где это уже разобрано. Возможно что-то похожее есть в книгах по сейсмологии.
Где сейчас остановился: Сейчас просмитриваю Аки Ричардса, но еще не нашел похожее. Не знаю или там найду. Так же есть наработки по аналогичной задаче, но на плоскости. Тут всплывают затруднения, т.к. уж слишком сложные формулы получаются для окружностей на сфере.
Жду помощи!
Найти точку на сфере
Добавлено: 22 окт 2013, 10:39
San1990
Все еще нужна помощь.
Найти точку на сфере
Добавлено: 22 окт 2013, 11:09
zam2
Имеется
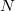
точек с координатами
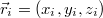
и точка-источник сигнала с коодинатами
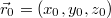
. В момент времени
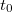
из точки
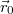
отправляются сигналы в направлении точек
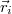
.

- время прихода сигнала в i-ю точку.
По известным

определить

.
Чем такая постановка задачи отличается от Вашей?
Найти точку на сфере
Добавлено: 22 окт 2013, 11:33
San1990
Очень интересная мысль. Возможно из нее как-то можно получить решение. Однако, в таком виде она не подходит. Вот контр пример: источник на северном полюсе, один датчик на эвкваторе и еще один датчик на южном полюсе. Волна от источника достигнет первого датчика за t, ну а второго, очевидно, за 2t. Но расстояние ко второму 2R, а к первому строго больше R.
P.S. Это сфера, а не шар. Поэтому сигналы всегда идут по поверхности.
Найти точку на сфере
Добавлено: 22 окт 2013, 11:49
zam2
То есть, источник и приемники на поверхности сферы, и сигналы распространяются по поверхности? А при чем тут сейсмология?
Расстояние от полюса до экватора

, от полюса до полюса

.
Найти точку на сфере
Добавлено: 22 окт 2013, 12:02
San1990
Ну, я подумал что вдруг там есть что-то похожее. Какие-нибудь работы.
Задача про сферу, а не шар. Поэтому только тонкая оболочка и поверхносные колебания.

- в этой формуле учитывается разница радиус-векторов. В результате получается вектор, а не дуга. Поэтому расстояние 2R, не pi*R. Или я не так понял.
Найти точку на сфере
Добавлено: 22 окт 2013, 12:12
zam2
San1990 писал(а):Source of the post 
- в этой формуле учитывается разница радиус-векторов. В результате получается вектор, а не дуга. Поэтому расстояние 2R, не pi*R. Или я не так понял.
Естественно, это не подходит. Я думал, что-то вроде задачи о локации центра землетрясения. Попробую написать новую версию.
Найти точку на сфере
Добавлено: 22 окт 2013, 13:10
San1990
Что скажете насчет такого. Воспользуемся системой приведенной выше.
Но наложем условие на радиус-вектор источника (4 уравнение).
4 неизвесных: 3 координаты и t1. Правда, не линейных.

Найти точку на сфере
Добавлено: 22 окт 2013, 13:51
zam2
Имеется
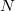
точек с координатами

и точка-источник сигнала с коодинатами

. В момент времени
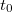
из точки
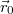
отправляются сигналы в направлении точек
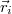
.

- время прихода сигнала в i-ю точку.
Здесь
![$$L_i=Rarccos\frac {[\vec{r_i},\vec{r_0}]} {R^2}$$ $$L_i=Rarccos\frac {[\vec{r_i},\vec{r_0}]} {R^2}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24L_i%3DRarccos%5Cfrac%20%7B%5B%5Cvec%7Br_i%7D%2C%5Cvec%7Br_0%7D%5D%7D%20%7BR%5E2%7D%24%24)
- длина дуги большого круга между точками
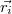
и
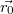
,
![$$[\vec{r_i},\vec{r_0}]$$ $$[\vec{r_i},\vec{r_0}]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5B%5Cvec%7Br_i%7D%2C%5Cvec%7Br_0%7D%5D%24%24)
- скалярное произведение векторов.
По известным

определить

.
Решением задачи будет решение системы уравнений:
![$$\{{cos( \frac {c(t_i-t_0)} {R})=\frac {[\vec{r_i},\vec{r_0}]} {R^2},i=1,...,N; \\ |\vec{r_0}|=R}$$ $$\{{cos( \frac {c(t_i-t_0)} {R})=\frac {[\vec{r_i},\vec{r_0}]} {R^2},i=1,...,N; \\ |\vec{r_0}|=R}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5C%7B%7Bcos%28%20%5Cfrac%20%7Bc%28t_i-t_0%29%7D%20%7BR%7D%29%3D%5Cfrac%20%7B%5B%5Cvec%7Br_i%7D%2C%5Cvec%7Br_0%7D%5D%7D%20%7BR%5E2%7D%2Ci%3D1%2C...%2CN%3B%20%5C%5C%20%7C%5Cvec%7Br_0%7D%7C%3DR%7D%24%24)
4 неизвестных, следовательно, достаточно трех точек наблюдения.
Вроде бы так.
San1990 писал(а):Source of the post Что скажете насчет такого. Воспользуемся системой приведенной выше.
Но наложем условие на радиус-вектор источника (4 уравнение).
4 неизвесных: 3 координаты и t1. Правда, не линейных.

Не пойдет. Расстояния нужно брать по дугам, а не по прямым.
Найти точку на сфере
Добавлено: 22 окт 2013, 14:27
San1990
Да, правильно! Я надеюсь))
И вообще, давайте для любого тела обобщим.

.
Остаётся только сделать функцию dist. Для сферы и плоскости это легко. Ну, а для цилиндра также возможно.
И еще сразу вопрос. Какими методами отбирать эти три точки если их больше. Например можно считать по трем точкам к которым сигнал пришел быстрее всего. Тоесть посортировать по времени и применить для первых трех.
Но возможно и как-то учитывать сигналы остальных для лучшей корекции. Данные эксперементальные и могуть быть (могут быть? точно будут) погрешности.
 . Где
. Где  - разница во времени прихода сигнала к і точки от времени прихода сигнала к первой. Тоесть когда появился сигнал мы не знаем. Но разницу между приходами сигнала к точкам мы знаем. (t3=>t2=>t1) Сфера единичная. Скорость распространения сигнала единичная. Нужно найти координаты точки от который был сигнал.
- разница во времени прихода сигнала к і точки от времени прихода сигнала к первой. Тоесть когда появился сигнал мы не знаем. Но разницу между приходами сигнала к точкам мы знаем. (t3=>t2=>t1) Сфера единичная. Скорость распространения сигнала единичная. Нужно найти координаты точки от который был сигнал.