Доказать предел (р.р. последовательности)
Добавлено: 11 окт 2013, 00:48
Пусть 
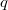 - иррациональное,
- иррациональное, ![$$A=[a, b] \subset [0, 1], I_A(x)$$ $$A=[a, b] \subset [0, 1], I_A(x)$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24A%3D%5Ba%2C%20b%5D%20%5Csubset%20%5B0%2C%201%5D%2C%20I_A%28x%29%24%24) - индикатор
- индикатор 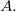
Доказать, что
Ясно, что сумма - это количество элементов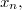 входящих в
входящих в 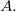
Хочу доказать, честно посчитав сумму (без критерия Вейли и прочего), но пока не могу найти опорных точек.
Предлагаю рассматривать
Доказать, что
Ясно, что сумма - это количество элементов
Хочу доказать, честно посчитав сумму (без критерия Вейли и прочего), но пока не могу найти опорных точек.
Предлагаю рассматривать