Касание кривых
Добавлено: 24 апр 2013, 03:05
ansm10
Уважаемые математики,
Две кривые заданы параметрически:


Кривые имеют касание в точке
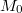
2-го порядка:
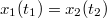
,
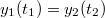

,

Будут ли эти кривые в точке
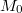
иметь одинаковые радиусы кривизны?
Касание кривых
Добавлено: 24 апр 2013, 12:15
vicvolf
Касание кривых
Добавлено: 24 апр 2013, 14:19
ansm10
Вот как я рассуждаю.

,

,

,

. Из уравнения радиуса кривизны видим, что они различаются. Верна ли логика?!
Касание кривых
Добавлено: 24 апр 2013, 15:02
Ian
Радиус кривизны не зависит от параметризации. Например, уменьшим масштаб времени в 2 раза, кривая будет проходиться в 2 раза быстрее а вторая производная вырастет в 4 раза. в итоге дробь из формулы 5 по ссылке -не изменится. Можно и строго доказать. Ну и при касании 2-го порядка радиусы кривизны либо одинаковы, либо бесконечны оба)
Касание кривых
Добавлено: 24 апр 2013, 16:16
ansm10
Ian писал(а):Source of the post Ну и при касании 2-го порядка радиусы кривизны либо одинаковы, либо бесконечны оба)
Если
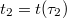
и новая параметризация такая, что

,
то дробь из формулы (5) по ссылке в обоих случая одинаковая.


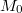 2-го порядка:
2-го порядка: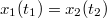 ,
, 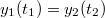
 ,
,
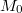 иметь одинаковые радиусы кривизны?
иметь одинаковые радиусы кривизны?