Пределы и доказательства
Пределы и доказательства
У меня возник вопрос общего характера. В определении предела числовой последовательности  и предела функции одной независимой переменной
и предела функции одной независимой переменной  фигурирует произвольное число
фигурирует произвольное число  . Можно ли при доказательстве утверждений о пределах брать
. Можно ли при доказательстве утверждений о пределах брать  , если
, если  (предел последовательности) и
(предел последовательности) и  , если
, если  (предел функции)? Думаю, что можно, так как число
(предел функции)? Думаю, что можно, так как число  произвольное. Или я неправ?
произвольное. Или я неправ?
Последний раз редактировалось Ellipsoid 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Поясню на примерах.
Задача №1. Доказать, пользуясь определением предела функции по Коши, что .
.
Зафиксируем произвольное . По определению правого предела нужно указать такое число
. По определению правого предела нужно указать такое число  , что из неравенства
, что из неравенства  следует
следует  . Учитывая, что
. Учитывая, что  , а значит, и
, а значит, и  , положим
, положим  . Тогда из неравенства
. Тогда из неравенства  следует
следует  .
.
Задача №2. Пусть . Доказать, что
. Доказать, что  .
.
Дано: . Доказать:
. Доказать:  . Учитывая, что
. Учитывая, что  , положим
, положим  , тогда
, тогда  и
и  при
при  .
.
Задача №1. Доказать, пользуясь определением предела функции по Коши, что
Зафиксируем произвольное
Задача №2. Пусть
Дано:
Последний раз редактировалось Ellipsoid 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Наоборот по  мы выбираем
мы выбираем 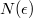 , что для всех n>N выполняется
, что для всех n>N выполняется 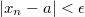 .
.
Последний раз редактировалось vicvolf 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Виктор В, мне кажется, Вы не совсем правильно поняли условие задачи: там дано, что  , поэтому
, поэтому  уже найдено. Не нужно доказывать, что
уже найдено. Не нужно доказывать, что  . Но, исходя из этого, нужно доказать, что
. Но, исходя из этого, нужно доказать, что  .
.
Последний раз редактировалось Ellipsoid 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Это место неубедительно. Вообще теорию пределов можно рассматривать как продолжение упражнений по школьной алгебре ( неравенства с параметрами), но с весьма узкими целями таких упражнений.
Вот я решаю задачу 2.
Пользуемся в одну сторону неравенствами типа
Получаем следствие из неравенства (*)
Ну и слова, понятно какие.
**UPD Тут еще проще
Последний раз редактировалось Ian 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Ian, cпасибо.
А почему неубедительно?
неубедительно?
Я решал эту задачу по-другому: , т.к. при
, т.к. при  всегда
всегда  . А этот способ придумал лишь как иллюстрацию к вопросу, содержащемуся в первом сообщении данной темы.
. А этот способ придумал лишь как иллюстрацию к вопросу, содержащемуся в первом сообщении данной темы.
А почему
Я решал эту задачу по-другому:
Последний раз редактировалось Ellipsoid 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
используйте, что
И пишите по возможности полный вариант док-ва исправленный, долго что ль из постов накопипастить.
Последний раз редактировалось Ian 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Хм... При  имеем
имеем  , значит,
, значит,  . При
. При  получим
получим  . Значит,
. Значит,  . Тогда
. Тогда  . Но если
. Но если  , то
, то  . :search:
. :search:
Хотя... Ведь из не следует, что
не следует, что  .
.
Хотя... Ведь из
Последний раз редактировалось Ellipsoid 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Я, не прочитав всего поста, взялся Вас поправлять. А эффективнее было бы поправить так:
Поэтому и прошу полный текст док-ва помещать, исправив старые опечатки и про них забыв
А надо было:
Найдите одно отличие, и почему Ваш текст неверен а мой верный., т.к. при
всегда
.
Поэтому и прошу полный текст док-ва помещать, исправив старые опечатки и про них забыв
Последний раз редактировалось Ian 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Пределы и доказательства
Ellipsoid вот я об этом и говорю - должно выполняться для всех n>N.
Последний раз редактировалось vicvolf 28 ноя 2019, 15:59, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей