Пределы
Добавлено: 24 дек 2011, 20:22
нашла свои институтские тетрадки, и что-то у меня не стыкуется, требуется ваша помощь, други.. ведь сами знаете, как быстро все забывается, с чем не сталкиваешься долго...
сначала пару глупых вопросов просто на основные моменты. Если не сложно, напомните какие-то главные правила, чтоб все в голове вернулось на свои места..

я вот вообще не понимаю - почему такой переход, почему к 1... почему нельзя было просто найти пределы от числителя и знаменателя и просто поделить? почему не . Или это у меня какой-то бред почему-то написан? или первый предел тоже к 1 был???
. Или это у меня какой-то бред почему-то написан? или первый предел тоже к 1 был???
да, уже почти уверена, что это описка была в первом пределе...
А вспоминать с таким бредом ещё хуже.. начинаешь вообще во всем сомневаться...
Лопиталить ведь можно только если в числителе и в знаменателе функции, пределы которых равны 0 или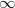 ? да?
? да?
вот если например такой предел:

он просто равен 0?
и вот застряли на 513 из Демидовича:

а предел

вроде как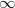 ?
?
а у Демидовича в ответе 1... т.е последний предел 0 д.б...
сначала пару глупых вопросов просто на основные моменты. Если не сложно, напомните какие-то главные правила, чтоб все в голове вернулось на свои места..
я вот вообще не понимаю - почему такой переход, почему к 1... почему нельзя было просто найти пределы от числителя и знаменателя и просто поделить? почему не
да, уже почти уверена, что это описка была в первом пределе...
А вспоминать с таким бредом ещё хуже.. начинаешь вообще во всем сомневаться...
Лопиталить ведь можно только если в числителе и в знаменателе функции, пределы которых равны 0 или
вот если например такой предел:
он просто равен 0?
и вот застряли на 513 из Демидовича:
а предел
вроде как
а у Демидовича в ответе 1... т.е последний предел 0 д.б...
