yourdomain.com

Доброго времени суток!
$$y''+2y'-3y=x^2 e^x $$

$k_{1}=\frac {-2-4} {2}=-3$
$k_{2}=\frac {-2+4} {2}=1$
$y=c_{1} e^{-3x} + c_{2} e^x$
$$f(x) = x^2 e^x $$

дальше для решения мне надо найти $\alpha$ и $\beta$
Но я не знаю откуда их найти(

частное решение надо искать в виде
$$y = x(ax^2+bx+c)e^x $$

подставить в уравнение и искать подходящие a,b,c

Что за $\alpha$ и $\beta$ ?
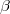
Сначала Вам надо найти, соответствует ли правая часть хотя бы одному корню характеристического уравнения и с учетом этого, построить общий вид частного решения неоднородного диффура с неизвестными коэффициентами и потом искать эти коэффициенты.

mihailm писал(а):Source of the post
частное решение надо искать в виде

подставить в уравнение и искать подходящие a,b,c

а разве не этой формулой ищут решение?
$y = x^r e^{\alpha x}(P_{l}(x)cos\beta x + Q_{l}(x)sin\beta x)$

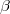
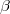
Да, по этой. Просто он уже $\alpha$ и $\beta$ подставил. Заодно могу сказать: $\alpha$ и $\beta$ - это просто коэффициенты при экспоненте и косинусе, соответственно. Брать их надо из правой части диффура.

Sonic86 писал(а):Source of the post
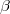
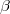
Да, по этой. Просто он уже $\alpha$ и $\beta$ подставил. Заодно могу сказать: $\alpha$ и $\beta$ - это просто коэффициенты при экспоненте и косинусе, соответственно. Брать их надо из правой части диффура.

а по какой формуле их вычислять из правой части?

Ни по какой. "Распознайте образ".
Правая часть имеет вид $$x^2e^x$$

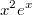
и правая часть имеет вид $e^{\alpha x}(P(x) \cos \beta x + Q(x) \sin \beta x)$ . Найдите отсюда коэффициенты и многочлены.

Sonic86 писал(а):Source of the post
Ни по какой. "Распознайте образ".
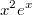
Правая часть имеет вид и правая часть имеет вид $e^{\alpha x}(P(x) \cos \beta x + Q(x) \sin \beta x)$ . Найдите отсюда коэффициенты и многочлены.

Альфа равна 1
Бетта равно 0
а $$Ax^2+Bx+C$$

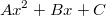
и берется как стандартная форумла так как в правой части уравнения Х²

Да.
Вторая греческая буква называется "бета".

Спасибо за то что помогли!
и не стоит придираться к тому как я пишу слова

yourdomain.com

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами

ЛНДУ II порядка с постоянными коэффициентами