Поверхностный интеграл второго рода
Добавлено: 21 май 2011, 10:58
Пусть есть поверхность заданная уравнением
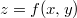
Необходимо вычислить поток через эту поверхность по внешней нормали, другими словами найти поверхностный интеграл второго рода.
Известна такая формула для сведения поверхностного интеграла второго рода к поверхностному интегралу первого рода:

С другой стороны, вектор нормали имеет коодинаты

Таким образом

Получили формулу сведения поверхностного интеграла к двойному
Но я такой формулы нигде в учебниках не виде :search: Верна ли она?
З.Ы Скобки почему то рисоваццо не хотят, но я думаю что ход понятен
Необходимо вычислить поток через эту поверхность по внешней нормали, другими словами найти поверхностный интеграл второго рода.
Известна такая формула для сведения поверхностного интеграла второго рода к поверхностному интегралу первого рода:
С другой стороны, вектор нормали имеет коодинаты
Таким образом
Получили формулу сведения поверхностного интеграла к двойному
Но я такой формулы нигде в учебниках не виде :search: Верна ли она?
З.Ы Скобки почему то рисоваццо не хотят, но я думаю что ход понятен