Ряд Маклорена
Добавлено: 13 янв 2011, 23:18
Здравствуйте!
Наткнулся на то же, что не могу решить.
Кто-нибудь может помочь мне в этом?
Сдача уже скоро, через два дня.
Спасибо
$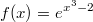
Разложить функцию в ряд Маклорена и найти область сходимости ряда?
Я так понимаю, что ряд Маклорена - частный случай ряда Тейлора, то есть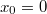
Как доказывать, что ряд сходится или расходится, помогите мне пожалуйста составить этот ряд для начала, ничего не получается.

Наткнулся на то же, что не могу решить.
Кто-нибудь может помочь мне в этом?
Сдача уже скоро, через два дня.
Спасибо
$
Разложить функцию в ряд Маклорена и найти область сходимости ряда?
Я так понимаю, что ряд Маклорена - частный случай ряда Тейлора, то есть
Как доказывать, что ряд сходится или расходится, помогите мне пожалуйста составить этот ряд для начала, ничего не получается.