Переход от дискретной системы к непрерывной
Добавлено: 19 сен 2010, 11:53
Добрый день!
Есть система уравнений вида:

где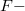 некая функция.
некая функция.
Хотелось бы свести данную сисему к одному интегральному уравнению вида:

Вопрос, как это правильно сделать, и как найти новые
Заранее благодарен!
Есть система уравнений вида:
где
Хотелось бы свести данную сисему к одному интегральному уравнению вида:
Вопрос, как это правильно сделать, и как найти новые
Заранее благодарен!