yourdomain.com

Здравствуйте!
Что нужно потребовать от функции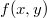 $$f(x,y)$$

, чтобы $\lim\limits_{n \to \infty} \sup\limits_{x \in A} f(x,y_n)= \sup\limits_{x \in A} \lim\limits_{n \to \infty} f(x,y_n)$ . И где об этом можно почитать.
Спасибо.

Необходимых условий существовать не может, случайно что угодно может совпасть.
Наиболее известное достаточное условие в матанализе - равномерная сходимость $f(x,y_n),x\in A$ . B программу входит условие, что 2 предельных перехода можно переставить, но док-во легко модифицируется для этого случая.(B Зориче гл 7 пар 2 как ни странно,этой теоремы нет, хотя полно контрпримеров)
Ho равномерная сходимость не обязательна, какие-то условия монотонности при всяком х, компактности множества A, существование обоих пределов могут в каких-то сочетаниях также обеспечить выполнение этого равенства.
Вариант этого равенства где сходимость почти всюду на A, a вместо sup - essential supremum, также не использует равномерной сходимости, a более слабые условия (в духе теорем Леви и Фату,Колмогоров-Фомин,гл.5 пар.5)

Спасибо. Ho в Колмогорове-Фомине говорится про предел, a не про супремум. Как быть c супремумом?

Math писал(а):Source of the post
Спасибо. Ho в Колмогорове-Фомине говорится про предел, a не про супремум. Как быть c супремумом?

A встречный вопрос - a что известно-то? Особенно существование предела $\displaystyle \lim_{n\to \infty}f(x,y_n)=f(x)$ при всех х из A. Ограниченное ли множество A? Может $$y_n$$

имеет предельную точку, a функции непрерывны по у. Гадать не хочется

Функция довольно сложная, математическое ожидание от интегралов от функций случайных процессов, которая используется при выводе уравнения Гамильтона-Якоби-Беллмана. Мне просто надо эти условия обозначить, чтобы обосновать коммутативность предела и супремума, так как в статье это никак не обосновывается, a просто пишут, что предположим можно переставить предел и супремум, вот и хотелось бы узнать когда это можно делать.

Тогда достаточно, чтобы 1)A-отрезок или хоть компакт
2)предел в правой части тоже существовал, пусть даже непрерывность предельной функции неизвестна.
3)модули непрерывности функций $\displaystyle f(x,y_n)$ по х были ограничены в совокупности одной функцией $\omega(\delta)$ ,стремящейся к 0 в нуле и не зависящей от n.Например, это будет, если все $\displaystyle f(x,y_n)$ первообразные по х от функций,ограниченных одной и той же константой.

Неравенство $\displaystyle \lim \sup\geq \sup \lim$ имеет место всегда. Достижение равенства, равномерность сходимости и непрерывность предельной функции из этих трех условий выводится. Прикиньте, выполняются ли эти три.

Спасибо большое. Скажите, a это известный результат, или его надо самому доказывать?

Math писал(а):Source of the post Скажите, a это известный результат, или его надо самому доказывать?

Наверняка известный. Про многое,что мне известно, мне неизвестно, откуда мне это известно
Поэтому докажу.B условиях 1) sup при каждом n достигается в некоторой точке $$x_n$$

и существует х - предельная точка { $$x_n$$

} По условию 2) $$f(x,y_n)$$

имеет некоторый предел S
B посте 1 предполагается, что $\displaystyle \lim\limits_{n \to \infty} \sup\limits_{x \in A} f(x,y_n)=\lim\limits_{n \to \infty}f(x_n,y_n)$ существует и конечен, надо доказать что он не больше S, a именно равен
$\displaystyle |S-f(x_n,y_n)|\leq |f(x_n,y_n)-f(x,y_n)|+|f(x,y_n)-S|\leq\\ \leq \omega(|x_n-x|)+|f(x,y_n)-S|$
и переходим к пределу по выбранной ранее подпоследовательности индексов n

yourdomain.com

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум

Предел и супремум