Однородное дифференциальное уравнение
Добавлено: 02 сен 2010, 20:34
Доброго времени суток.
Имеется уравнение:

Если я правильно определил, то это однородное диф уравнение.
Пытаюсь решить методом замены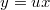 , получается:
, получается:

Привести выражение к уравнению c разделяющимися переменными не получается или я что-то упускаю из виду.
Попробовал следующий способ:
Известно, что:

Тогда:
 ;
;

Произвожу замену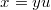 ;
;  ;
;
 ;
;
 ;
;
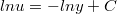 ;
;
a т.к.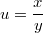 , то
, то 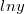 сокращается и остаётся
сокращается и остаётся 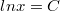 .
.
Хотелось бы узнать, верно ли это решение?
Имеется уравнение:
Если я правильно определил, то это однородное диф уравнение.
Пытаюсь решить методом замены
Привести выражение к уравнению c разделяющимися переменными не получается или я что-то упускаю из виду.
Попробовал следующий способ:
Известно, что:
Тогда:
Произвожу замену
a т.к.
Хотелось бы узнать, верно ли это решение?