Прошу помощи!
Добавлено: 26 апр 2010, 07:38
Помогите, пожалуйста. Нужно скоро сдать задачу, a у меня никак не получается. Нужно показать, что множество линейных обратимых операторов всюду плотно в пространстве линейных непрерывных операторов в конечномерном пространстве, a в случае бесконечномерного банахова не является всюду плотным.
Заранее благодарю всех откликнувшихся.
Всюду плотное множество -значит для любого элемента A всего пространства существует последовательность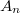 элементов из множества, стремящаяся к A по норме. Возьмем произвольный оператор A
элементов из множества, стремящаяся к A по норме. Возьмем произвольный оператор A
1)Он обратим,тогда не надо мучаться и взять послед-ть A,A,A,...
2)Он необратим (то есть 0-точка его спектра,=собственное число).Возьмем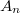 как в посте,они обратимы,так как ни одно из лямбд не является собственным числом. Норма разности
как в посте,они обратимы,так как ни одно из лямбд не является собственным числом. Норма разности  .
.
Вот и доказали что обратимые операторы всюду плотны.
Заранее благодарю всех откликнувшихся.
Всюду плотное множество -значит для любого элемента A всего пространства существует последовательность
1)Он обратим,тогда не надо мучаться и взять послед-ть A,A,A,...
2)Он необратим (то есть 0-точка его спектра,=собственное число).Возьмем
Вот и доказали что обратимые операторы всюду плотны.