Привести пример множества.
Добавлено: 25 фев 2010, 19:05
Задача из "Общей топологии" Бурбаки:
Для каждого множества A положим Привести пример множества A на числовой прямой, для которого семь множеств
Привести пример множества A на числовой прямой, для которого семь множеств  попарно различны. Задача имеет продолжение, но в данном случае оно несущественно; лучшеe, до чего я смог додуматься, был полуоткрытый интервал c "выколотым" счетным множеством, но в этом случае
попарно различны. Задача имеет продолжение, но в данном случае оно несущественно; лучшеe, до чего я смог додуматься, был полуоткрытый интервал c "выколотым" счетным множеством, но в этом случае 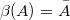 т.e. не удовлетворяет условиям задачи. Заранеe благодарю за любые идеи.
т.e. не удовлетворяет условиям задачи. Заранеe благодарю за любые идеи.
P.S.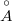 - внутрнность множества - объединение всех открытых множеств, принадлежщих A, максимальное открытое множество, принадлежащеe A.
- внутрнность множества - объединение всех открытых множеств, принадлежщих A, максимальное открытое множество, принадлежащеe A.
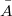 - замыкание множества A
- замыкание множества A
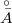 - внутрнность замыкания
- внутрнность замыкания
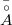 - замыкание внутренности
- замыкание внутренности
Для каждого множества A положим
P.S.