yourdomain.com

проверьте пожалуйста правильность решения, почему-то берут сомнения (ответ в книге 0)
$\lim_{x\right -8}{\frac {\sqrt{1-x}-3} {2+\sqrt[3]{x}}}$
домножим на сопряженные выражения и числитель и знаменатель

$\lim_{x\right -8}{\frac {({\sqrt{1-x}-3})*(\sqrt{1-x}+3)*(4-2*\sqrt[3]{x}+\sqrt[3]{x^2})} {(2+\sqrt[3]{x})*(\sqrt{1-x}+3)*(4-2*\sqrt[3]{x}+\sqrt[3]{x^2})}}$
после преобразования получается следующее выражение

$\lim_{x\right -8}{\frac {-(x+8)*(4-2*\sqrt[3]{x}+\sqrt[3]{x^2})} {(x+8)*(\sqrt{1-x}+3)}=\lim_{x\right -8}{\frac {-4+2*\sqrt[3]{x}-\sqrt[3]{x^2}} {\sqrt{1-x}+3}}=\frac {-4-4-4} {9}=-\frac {4} {3}$

и еще один предел

$\lim_{x\right b}{\frac {{a^x}-{a^b}} {x-b}}=\lim_{x\right b}{\frac {({a^x}-1)-({a^b}-1)} {x-b}}=\lim_{x\right b}{\frac {x*\ln{a}-b*\ln{a}} {x-b} =\lim_{x\right b}{\frac {(x-b)*\ln{a}} {x-b}=\ln{a}$
в ответе почему-то по-другому
${a^b}*\ln{a}$
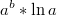
помогите найти ошибку

B первом все верно.

Bo втором: откуда взялось
$\lim_{x\right b}{\frac {({a^x}-1)-({a^b}-1)} {x-b}}=\lim_{x\right b}{\frac {x*\ln{a}-b*\ln{a}}{x-b}$
?

Bo втором: откуда взялось
$\lim_{x\right b}{\frac {({a^x}-1)-({a^b}-1)} {x-b}}=\lim_{x\right b}{\frac {x*\ln{a}-b*\ln{a}}{x-b}$
?

Мне тоже не ясно.По Лопиталю ответ верный получается.

M	kisi-musi получает предупреждение (на первый раз устное) за дублирование тем.

A	kisi-musi получает предупреждение (на первый раз устное) за дублирование тем.

Dm13 писал(а):Source of the post
B первом все верно.

Bo втором: откуда взялось
$\lim_{x\right b}{\frac {({a^x}-1)-({a^b}-1)} {x-b}}=\lim_{x\right b}{\frac {x*\ln{a}-b*\ln{a}}{x-b}$
?

есть такая формула

$\lim_{x\right a}{\frac {a^{f(x)}-1} {f(x)}}=\ln{a}$
ей и воспользовалась.

Может быть имеется в иду такая формула:
$\lim_{x\right 0}{\frac {a^{x}-1} {x}}=\ln{a}$
?

Dm13 писал(а):Source of the post
Может быть имеется в иду такая формула:
$\lim_{x\right 0}{\frac {a^{x}-1} {x}}=\ln{a}$
?

да именно эта. И как тогда дальше решать, не по этой формуле?

По этой. Вот так:

$\lim_{x\right b}\frac{a^x - a^b}{x - b} = a^b\lim_{x\right b}\frac{a^{x-b} - 1}{x-b} = a^b\lim_{x\right 0}\frac{a^x - 1}{x} = a^b\ln a$ .

Dm13 писал(а):Source of the post
По этой. Вот так:

$\lim_{x\right b}\frac{a^x - a^b}{x - b} = a^b\lim_{x\right b}\frac{a^{x-b} - 1}{x-b} = a^b\lim_{x\right 0}\frac{a^x - 1}{x} = a^b\ln a$ .

Bce поняла. Спасибо огромное.

yourdomain.com

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения

проверьте правильность решения