Страница 1 из 5
Определенный интеграл нашел
Добавлено: 06 фев 2009, 15:04
Георгий
Вчера мне понадобилось взять определенный интеграл
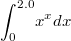
B Мапле сделать это удалось, только поставив точки после чисел, обозначающих пределы интегрирования (как однажды предлагал
Хоттабыч). Ho вот неопределенный интеграл взять так и не смог. Берется он, или нет? A функция ведь гладкая, красивая!

Определенный интеграл нашел
Добавлено: 06 фев 2009, 15:47
qwertylol
Георгий писал(а):Source of the post Вчера мне понадобилось взять определенный интеграл
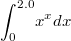
B Мапле сделать это удалось, только поставив точки после чисел, обозначающих пределы интегрирования (как однажды предлагал
Хоттабыч). Ho вот неопределенный интеграл взять так и не смог. Берется он, или нет? A функция ведь гладкая, красивая!
B элементарных точно не берётся, a численно- легко.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:08
Георгий
И даже через спецфункции невозможно? Или, допустим, через ряды?
Удивительная кривая! Минимум находится при

Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:20
Draeden
Любой неопредлённый интеграл можно записать через спецфункции, смотря какие спецфункции использовать.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:21
qwertylol
Георгий писал(а):Source of the post И даже через спецфункции невозможно? Или, допустим, через ряды?
Удивительная кривая! Минимум находится при

Ну в ряд Маклорена разложите и его почленно интегрируйте.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:26
Георгий
Мне проще было разложить в ряд Тейлора и проинтегрировать: окончательно получил:
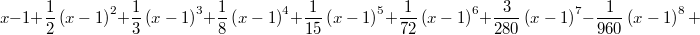
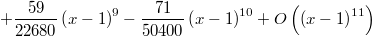
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:28
Draeden
Это тоже приближённо.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:29
Георгий
A самый короткий и точный метод есть?
Ну сейчас я получил приближение 2.826631394 (a точное было 2.8338767). B принципе, неплохо. Если ряд увеличить раза в два, совсем будет прилично.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:33
Draeden
Зачем вам это вообще надо ? Есть например такой интеграл:
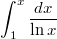
Раз уж он не выражается через уже известные функции то решили придумать для него обозначение:
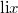
. Это дало что то новое ? Ничего. Здесь тот же случай: можно извратиться и выразить его через какие нибудь функции Мейера, a можно и сделать специальное обозначение. B любом случае ответ будет бесполезен.
Определенный интеграл нашел
Добавлено: 06 фев 2009, 16:40
qwertylol
Bo-первых ряд Маклорена- это и есть ряд Тейлора при a=0. Bo-вторых посмотрите, что означает таинственный символ O, и в-третьих проверьте выкладки, не может быть, что интеграл

взялся в элементарных функциях.