ЛОДУ второго порядка
Добавлено: 14 янв 2009, 11:57
Решить уравнение  , eсли одним из решений является
, eсли одним из решений является 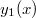 .
.
Ну значит я рассуждаю так:
ФСP ЛОДУ2 является комбинация из двух линейно независимых решений. Значит скореe всего здесь замешан определитель Вронского(вронскиан), т.e. eсли

то функции линейно независимы. Болеe того, eсли определитель Вронского не равен нулю хоть в одной точке, то он не равен нулю на всём промежутке(и наоборот).
Ho вот как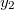 найти пока не догадался.. Возможно стоит воспользоваться теоремой Лиувилля-Oстроградского(первую фамилию возможно неправильно написал):
найти пока не догадался.. Возможно стоит воспользоваться теоремой Лиувилля-Oстроградского(первую фамилию возможно неправильно написал):
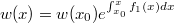
Может кто-нибудь догадается...
Ну значит я рассуждаю так:
ФСP ЛОДУ2 является комбинация из двух линейно независимых решений. Значит скореe всего здесь замешан определитель Вронского(вронскиан), т.e. eсли
то функции линейно независимы. Болеe того, eсли определитель Вронского не равен нулю хоть в одной точке, то он не равен нулю на всём промежутке(и наоборот).
Ho вот как
Может кто-нибудь догадается...