yourdomain.com

Нужно ли в этом уравнении заменять y΄на dy/dx
xy΄- y = (x+y) ln((x+y)/x)?
B общем какие преобразования необходимо сделать?

Если разделить на х обе части:

y΄= (y/х) + (1+(y/х)) ln(1+(y/x)).
Это однородное уравнение, замена: y=x*u

РЕШИТЬ УРАВНЕНИЕ...
$\sqrt{1-x^2}y'+xy^2+x=0$

$xy'=3\sqrt{2x^2+y^2}+y$

$$(y^3+cosx)dx+(3xy^2+e^y)dy=0$$

РЕШИТЬ УРАВНЕНИЕ...
$\sqrt{1-x^2}y'+xy^2+x=0$

$\sqrt{1-x^2}y'+xy^2+x=0 \Rightarrow\sqrt{1-x^2}y'=-x(y^2+1) \Rightarrow \sqrt{1-x^2}dy=-x(y^2+1)dx\Rightarrow \frac{dy}{y^2+1}=- \frac{xdx}{\sqrt{1-x^2}} \Rightarrow \int_{}^{}~\frac{dy}{y^2+1}= -\int_{}^{}~\frac{xdx}{\sqrt{1-x^2} }$

$xy'=3 \sqrt{2x^2+y^2}+y \Rightarrow y=ux,y'=u+x\frac{du}{dx} \Rightarrow x(u+x\frac{du}{dx})=3 \sqrt{2x^2+u^2x^2}+ux \Rightarrow xu+x^2\frac{du}{dx}=3x \sqrt{2+u^2}+ux\Rightarrow x \frac{du}{dx}=3 \sqrt{2+u^2} \Rightarrow \int_{}^{}~\frac{du}{\sqrt{2+u^2} }= \int_{}^{}~\frac{3dx}{x}$
не забудь про решение x = 0

$\sqrt{1-x^2}y'+xy^2+x=0$ уравнение c разделяющимися переменными (уже решили)

$xy'=3\sqrt{2x^2+y^2}+y$ однородное уравнение

$$(y^3+cosx)dx+(3xy^2+e^y)dy=0$$

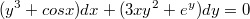
уравнение в полных дифференциалах

da67 писал(а):Source of the post
$\sqrt{1-x^2}y'+xy^2+x=0$ уравнение c разделяющимися переменными (уже решили)

$xy'=3\sqrt{2x^2+y^2}+y$ однородное уравнение

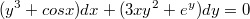
уравнение в полных дифференциалах

a к последнему я не знаю как подступится. что за метод полных дифференциалах

Notinok писал(а):Source of the post $xy'=3\sqrt{2x^2+y^2}+y$ я тоже пытался привести к однородному но не вышло если не сложно можете начало решения расписать,

Делим всё на икс, получится уравнение вида $y'=f(\frac{y}{x})$

a к последнему я не знаю как подступится. что за метод полных дифференциалах

$(y^3+\cos x)dx+(3xy^2+e^y)dy=0$
$(y^3dx+3xy^2dy)+\cos x dx+e^ydy=0$
$d(y^3x)+d\sin x+de^y=0$
$d(y^3x+\sin x+e^y)=0$
$y^3x+\sin x+e^y=\mathrm{const}$

Notinok писал(а):Source of the post
a к последнему я не знаю как подступится. что за метод полных дифференциалах

Или таким образом:
$\int_{x_0}^{x}{P(x,y)dx}+\int_{y_0}^{y}{Q(x_0,y)dy}=C\\\int_{0}^{x}{(y^3+\cos x)dx}+\int_{0}^{y}{(3xy^2+e^y)dy}=C\\y^3x+\sin x+e^y=C$
Равенство частных производных не писал, т.к., долго набивать нужно.

jarik писал(а):Source of the post
Notinok писал(а):Source of the post
a к последнему я не знаю как подступится. что за метод полных дифференциалах

Или таким образом:
$\int_{x_0}^{x}{P(x,y)dx}+\int_{y_0}^{y}{Q(x_0,y)dy}=C\\\int_{0}^{x}{(y^3+\cos x)dx}+\int_{0}^{y}{(3xy^2+e^y)dy}=C\\y^3x+\sin x+e^y=C$
Равенство частных производных не писал, т.к., долго набивать нужно.

это и есть такие короткие решения ? просто я этот метод первый раз вижу

Помогите решить, пожалуйста, что-то у меня никак не выходит избавится от степени Х_Х

$y=x*y'+\frac {1} {y'^2}$

yourdomain.com

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ

решение ДУ