Страница 1 из 2
Несложный предел
Добавлено: 29 дек 2007, 22:19
Draeden
Мы в школе начали проходить пределы, пытались на уроке решить такую задачку:

но у нас ничего не получилось
Несложный предел
Добавлено: 29 дек 2007, 23:40
vladb314
И правда несложный. Mathematica выдаёт e/2
Несложный предел
Добавлено: 29 дек 2007, 23:44
Draeden
хммм... я считал его устно и получил

, наверно гдето ошибся :search:
Несложный предел
Добавлено: 30 дек 2007, 19:27
Draeden
Неужели никто не предложит решение ?
Несложный предел
Добавлено: 30 дек 2007, 20:31
AV_77

Применяем правило Лопиталя:

Вроде нигде не ошибся.
Несложный предел
Добавлено: 30 дек 2007, 20:41
Draeden
эээ... в знаменателе стоит

a не

, хотя ответ верный.
Несложный предел
Добавлено: 30 дек 2007, 20:43
AV_77
Да, опечатался. Уже исправил.
Несложный предел
Добавлено: 30 дек 2007, 21:00
Draeden
Ну чтож, предел решён (я предполагал разложение в ряд Тейлора, но AV_77 вычислил предел проще).
Предлагаю такую задачу:

вычислить

.
Несложный предел
Добавлено: 30 дек 2007, 21:26
a_l_e_x86
Если предположить что функция дифференцируема, и взять производную от обеих частей, получим


, следовательно

или
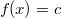
.
Таким образом f(0)=c, где c - корень уравнения
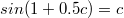
Несложный предел
Добавлено: 30 дек 2007, 21:28
vladb314
Да, причем численное его значение c = 0,997402...
