но у нас ничего не получилось
Несложный предел
Несложный предел
Мы в школе начали проходить пределы, пытались на уроке решить такую задачку:

но у нас ничего не получилось
но у нас ничего не получилось
Последний раз редактировалось Draeden 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
И правда несложный. Mathematica выдаёт e/2
Последний раз редактировалось vladb314 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
хммм... я считал его устно и получил  , наверно гдето ошибся :search:
, наверно гдето ошибся :search:
Последний раз редактировалось Draeden 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Неужели никто не предложит решение ?
Последний раз редактировалось Draeden 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Применяем правило Лопиталя:
Вроде нигде не ошибся.
Последний раз редактировалось AV_77 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
эээ... в знаменателе стоит  a не
a не  , хотя ответ верный.
, хотя ответ верный.
Последний раз редактировалось Draeden 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Да, опечатался. Уже исправил.
Последний раз редактировалось AV_77 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Ну чтож, предел решён (я предполагал разложение в ряд Тейлора, но AV_77 вычислил предел проще).
Предлагаю такую задачу:

вычислить .
.
Предлагаю такую задачу:
вычислить
Последний раз редактировалось Draeden 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Если предположить что функция дифференцируема, и взять производную от обеих частей, получим

 , следовательно
, следовательно
 или
или 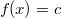 .
.
Таким образом f(0)=c, где c - корень уравнения
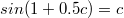
Таким образом f(0)=c, где c - корень уравнения
Последний раз редактировалось a_l_e_x86 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Несложный предел
Да, причем численное его значение c = 0,997402...
Последний раз редактировалось vladb314 30 ноя 2019, 13:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 10 гостей