Всё теже излюбленные РЯДЫ (Мать ИХ)
Добавлено: 28 май 2007, 22:53
Блин поможите пож... Уже МОЗГ кипит .....
#1
#2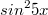
#3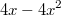 по степ. (x+2)
по степ. (x+2)
#4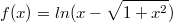
PS: ОЧ.... нужно !!!
#1
#2
#3
#4
PS: ОЧ.... нужно !!!
Краткое описание форума
http://e-science11.ru/test_forum/
deshi писал(а):Source of the post
Блин поможите пож... Уже МОЗГ кипит .....
#1
#2
#3по степ. (x+2)
#4
PS: ОЧ.... нужно !!!