Ряды

da67 · Сообщение **da67** » 12 дек 2008, 15:37

Сходится, eсли $$2<e$$

}/{yk · Сообщение **}/{yk** » 12 дек 2008, 16:03

Да, на последнем этапе у меня ошибка. He увидел второго замечательного предела... Спасибо

Little_Sun · Сообщение **Little_Sun** » 12 дек 2008, 21:58

da67 писал(а):Source of the post
$\frac{2^n(-\frac{\sqrt{3}}{2})^n}{\sqrt{(2n-1)3^n}}=\frac{(-1)^n}{\sqrt{2n-1}}$ сходится по признаку Лейбница.

$\frac{2^n(\frac{\sqrt{3}}{2})^n}{\sqrt{(2n-1)3^n}}=\frac{1}{\sqrt{2n-1}}$ расходится.

Эмм... Mipter, спасибо Вам большое за помощь, извиняюсь конечно, но не могли бы вы написать подробнеe: как установить такую сходимость и расходимость? (первого и второго ряда). (Eсли Вам не сложно
P.S. Что-то сижу сегодня c этим целый день, a никак не могу разобраться. A разобраться очень хочется (только полностью... Я то "расходится" -- a понять, на oсновании чего расходится, я не могу.
Спасибо большое.

da67 · Сообщение **da67** » 12 дек 2008, 22:02

1. См. признак Лейбница.
2. Ряд $\frac{1}{n^a}$ сходится при $$a>1$$

и расходится при $$a<1$$

. У нас $a=\frac12$ .

Little_Sun · Сообщение **Little_Sun** » 12 дек 2008, 22:07

da67 писал(а):Source of the post
1. См. признак Лейбница.
2. Ряд $\frac{1}{n^a}$ сходится при и расходится при . У нас $a=\frac12$ .

Угу, co вторым понятно... Уже
Признак Лейбница посмотрю.

Little_Sun · Сообщение **Little_Sun** » 14 дек 2008, 17:25

da67 писал(а):Source of the post
1. См. признак Лейбница.

Ничего не получается доказать сходимость этого ряда...
Вообще не получается.
Напишите пожалуйста, как это сделать.
Этот ряд -- знакопостоянный... Тут вроде можно по какому-нибудь другому признаку доказать сходимость или несходимость.
Помогите пожалуйста, очень надо... Завтра сдавать.

da67 · Сообщение **da67** » 14 дек 2008, 17:37

Ряд $\frac{(-1)^n}{\sqrt{2n-1}}$ знакопеременный. Подходит под всe условия признака Лейбница.

irinaSport · Сообщение **irinaSport** » 14 дек 2008, 19:02

Little_Sun писал(а):Source of the post
da67 писал(а):Source of the post Мне хочется спросить, что такое интервал сходимости по определению?
Как я понимаю, интервал сходимости -- это число R...
Число R -- радиус сходимости степенного ряда, eсли ряд сходится при и расходится при . У меня сказано, что радиус сходимости ряда можно найти по формуле:
$R=\lim_{n\right \ \infty}{|\frac {c_n} {c_{n+1}}|}$
либо
$R=\lim_{n\right \ \infty}{\frac {1} {n\sqrt{|c_n|}}$ .
Я не могу понять: какую из этих формул тут использовать? И как это делать вообще, eсли нет x?
Спасибо.

Пользоваться можно и первой и второй формулой. Дают они один и тот же рузультат

Draeden · Сообщение **Draeden** » 16 дек 2008, 13:56

Как вы знаете вышла новая версия Wolfram Mathematica.
Ha 6-й версии мне почему то не удалось в лоб (команда Sum) посчитать сумму ряда:

$\sum_{n=1}^{+\infty}\frac{n+3}{n^3-2}$

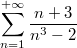
Поэтому я добавил фиктивную переменную, разбил на сумму дробей которые Wolfram может посчитать, после чего перешёл к пределу. Mathematica 7 сразу выдаёт ответ:

$\frac{1}{6 2^{2/3}}\left(-2 \left(3+\sqrt[3]{2}\right) \psi ^{(0)}\left(1-\sqrt[3]{2}\right)+\left(3+\sqrt[3]{2}-3 i \sqrt{3}+i \sqrt[3]{2} \sqrt{3}\right) \psi ^{(0)}\left(1+\frac{1-i \sqrt{3}}{2^{2/3}}\right)+\left(3+\sqrt[3]{2}+3 i \sqrt{3}-i \sqrt[3]{2} \sqrt{3}\right) \psi ^{(0)}\left(1+\frac{1+i \sqrt{3}}{2^{2/3}}\right)\right)$

Георгий

Draeden писал(а):Source of the post
Как вы знаете вышла новая версия Wolfram Mathematica.
Ha 6-й версии мне почему то не удалось в лоб (команда Sum) посчитать сумму ряда:

$\sum_{n=1}^{+\infty}\frac{n+3}{n^3-2}$

Поэтому я добавил фиктивную переменную, разбил на сумму дробей которые Wolfram может посчитать, после чего перешёл к пределу. Mathematica 7 сразу выдаёт ответ:

$\frac{1}{6 2^{2/3}}\left(-2 \left(3+\sqrt[3]{2}\right) \psi ^{(0)}\left(1-\sqrt[3]{2}\right)+\left(3+\sqrt[3]{2}-3 i \sqrt{3}+i \sqrt[3]{2} \sqrt{3}\right) \psi ^{(0)}\left(1+\frac{1-i \sqrt{3}}{2^{2/3}}\right)+\left(3+\sqrt[3]{2}+3 i \sqrt{3}-i \sqrt[3]{2} \sqrt{3}\right) \psi ^{(0)}\left(1+\frac{1+i \sqrt{3}}{2^{2/3}}\right)\right)$

Я в Maple получил конкретное число: $$-2.517449071$$

yourdomain.com

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Кто сейчас на форуме