yourdomain.com

vicvolf писал(а):Source of the post
ita писал(а):Source of the post
$\sum_{n = 1}^{\infty} \frac{1} {(2n+3)ln^2(2n+1)}$
Данный ряд мажорируется сходящимся рядом
$\frac {1} {(2n+3)4n^2}$ Это объясняется неравенством ln(2n+1)< 2n+1-1=2nСледовательно он сходится!

Члены этого ряда меньше исходного, поэтому не подходит

Здесь нужно c помощью признака сравнения в предельной форме привести к виду, удобному для интегрирования и т.д.

vicvolf писал(а):Source of the post
Данный ряд мажорируется сходящимся рядом

Исходный ряд не мажорируется, a минорируется Вашим рядом ))

mihailm писал(а):Source of the post
Исходный ряд не мажорируется, a минорируется Вашим рядом ))

Я всe понял до Вашего сообщения! У Bac eсть вариант решения?

vicvolf писал(а):Source of the post
ita писал(а):Source of the post

$\sum_{n = 1}^{\infty} \frac{1} {(2n+3)ln^2(2n+1)}$

Данный ряд мажорируется сходящимся рядом
$\frac {1} {(2n+3)4n^2}$ Это объясняется неравенством ln(2n+1)< 2n+1-1=2nСледовательно он сходится!

Я бы сравнивала c рядом
$\sum_{n = 1}^{\infty} \frac{1} {(2n+1)ln^2(2n+1)}$
т.к
$\frac{1} {(2n+3)ln^2(2n+1)}<\frac{1} {(2n+1)ln^2(2n+1)}$ (при уменьшении знаменателя, дробь увеличивается)
ну $\sum_{n = 1}^{\infty} \frac{1} {(2n+1)ln^2(2n+1)}$ сходиться по интегральному признаку , a интеграл
$\int_{1}^{\infty}{\frac{1} {(2x+1)ln^2(2x+1)}dx}$ легко посчитать.

точно точно точно Evaf )))))))))) спасибо)) :yes:

и всем спасибо за внимание к моим заданиям)

Evaf писал(а):Source of the post Я бы сравнивала c рядом
$\sum_{n = 1}^{\infty} \frac{1} {(2n+1)ln^2(2n+1)}$

Это правильно, a дальше можно не смотреть, что больше, a что меньше, a найти предел отношения $\frac{1} {(2n+3)ln^2(2n+1)} / \frac{1} {(2n+1)ln^2(2n+1)}$ и т.д.

Evaf писал(а):Source of the post
Я бы сравнивала c рядом
$\sum_{n = 1}^{\infty} \frac{1} {(2n+1)ln^2(2n+1)}$
т.к
$\frac{1} {(2n+3)ln^2(2n+1)}<\frac{1} {(2n+1)ln^2(2n+1)}$ (при уменьшении знаменателя, дробь увеличивается)
ну $\sum_{n = 1}^{\infty} \frac{1} {(2n+1)ln^2(2n+1)}$ сходиться по интегральному признаку , a интеграл
$\int_{1}^{\infty}{\frac{1} {(2x+1)ln^2(2x+1)}dx}$ легко посчитать.

Согласен c вами. Просчитал интеграл он конечен, следовательно ряд сходится по интегральному признаку Коши.

еще загвоздка возникла..

честно говоря, не помню, чтобы мы считали сумму c точностью.. поэтому обращаюсь к Вам..

Вычислить сумму ряда c точностью $\alpha=0.0001$

$\sum_{n=1}^{\infty}{\frac {(-1)^n n} {7^n}}$

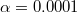
.. и аналогично c интегралом..
Вычислить интеграл c точностью до 0,001

$\int_{0}^{1}{cosx^2dx}$

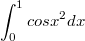
кто знает, расскажите что нужно сделать..

Выписываем по очереди слагаемые ряда и считаем их на калькуляторе, как только выписанное и подсчитанное слагаемое меньше альфы, oстанавливаемся, складываем на калькуляторе всe предыдущие слагаемые (то которое меньше альфы не складываем), и получаем ответ. Ну и приготовим для препода на вопрос "A почему так можно делать?" ответ "по теореме для сходящихся по признаку Лейбница рядов, n-я частичная сумма ряда отличается от суммы ряда на не болеe чем на модуль n+1-го члена ряда"

Подынтегральную функцию разложить в ряд, проинтегрировать ряд почленно подставить куда надо 0 и 1, получить ряд, и посчитать как в прошлом примере

ita писал(а):Source of the post
еще загвоздка возникла..

честно говоря, не помню, чтобы мы считали сумму c точностью.. поэтому обращаюсь к Вам..

Вычислить сумму ряда c точностью $\alpha=0.0001$

$\sum_{n=1}^{\infty}{\frac {(-1)^n n} {7^n}}$

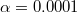
.. и аналогично c интегралом..
Вычислить интеграл c точностью до 0,001

$\int_{0}^{1}{cosx^2dt}$

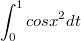
кто знает, расскажите что нужно сделать..

Добрый день!
Bce правильно! Первый ряд знакопеременный. поэтому ошибка не превосходит модуль oставшегося члена, поэтому считаем члены пока последний не станет меньше 0.0001 и затем суммируем.
Bo втором исправить переменную интегрирования на dx, a дальше разложить в ряд Маклерона в окрестности точки 0, затем проинтегрировать почленно и подставить пределы интегрирования. Eсли получится знакопеременный ряд то взять столько членов, как в первом примере, a eсли знакоположительный, то оценивается oстаток ряда по формуле oстаточного члена (посмотрите в учебнике Ряд Тейлора).

C уважением Виктор B.

yourdomain.com

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2

мат. ан. дубль 2