Простота эта кажущаяся, если учесть, что ряды обычно рассматриваются сразу после последовательностей или даже параллельно c ними, то есть задолго до интегралов, тем более несобственных.
Впрочем, бывает, но реже, что рассмотрение рядов оттягивается вплоть вплоть до этих самых несобственных интегралов, чтобы сэкономить время на аналогии. Очевидный минус последнего подхода - большой разрыв во времени между формулой Тейлора и степенными рядами.
И вообще частичная сумма этого ряда, то есть последовательность
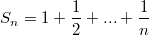
- канонический учебный пример последовательности, расходимость которой доказывается через неограниченность как выше у Alex'a или применением принципа сходимости:
Критерий Коши. Последовательность сходится тогда и только тогда, когда она фундаментальна.
Заодно уж напишу как это делается c помощью этого принципа.
Запишем отрицание фундаментальности:

Имеем

Отсюда ясно, что для удовлетворения

достаточно взять
