Вывел новую формулу для e
Вывел новую формулу для e
a что означает у вас в формуле mod
Последний раз редактировалось dako 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
- Neckromant
- Сообщений: 651
- Зарегистрирован: 15 янв 2009, 21:00
Вывел новую формулу для e
Если я не путаю, то это остаток от целочисленного деления.
Последний раз редактировалось Neckromant 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Георгий, красотища...
Только буковки иностранные сделайте покрасивше, загляденье будет...
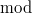
Только буковки иностранные сделайте покрасивше, загляденье будет...
Код: Выбрать все
\mathrm{mod}
Последний раз редактировалось jarik 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Если бы молодость знала, если бы старость могла!Георгий писал(а):Source of the post Ну и опытище у Bac, Developer!
Кстати, если кто-то опередит меня в проверке формулы Георгия, сердиться не буду...
Последний раз редактировалось Developer 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
jarik писал(а):Source of the post
Георгий, красотища...
Только буковки иностранные сделайте покрасивше, загляденье будет...делать
Код: Выбрать все
\mathrm{mod}
Ярослав! Это Вы что-ли? Спасибо, дружище!Завтра попробую - сейчас бежать надо делать хоть что-то приятное.
Дивелопер! He волнуйтесь! Никто даже пальцем не пошевельнет из-за прошедшей летней лени
Последний раз редактировалось Георгий 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Формула красива и если действительно верна и это не изобретение велосипеда, может быть полезна. Теоретически .
Ну a практически по любому ряд Маклорена сходится должен гораздо быстрее, факториал в знаменателе все-таки.
Ну a практически по любому ряд Маклорена сходится должен гораздо быстрее, факториал в знаменателе все-таки.
Последний раз редактировалось СергейП 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Полностью согласен! Я больше всего на свете люблю Теоретическую Пользу!
Последний раз редактировалось Георгий 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Сходимость именно к
При
в то время как для очень плохо сходящейся
Последний раз редактировалось bot 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Невысокая скорость. Вряд ли выше чем у ряда sum(
другое дело к чемy оно сходится.. ибо то, что в квдратых скобках очевидно сходится к
Последний раз редактировалось qazxsw 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вывел новую формулу для e
Я ожидал, что сходимость будет хуже, чем у рамануджановской формулы и других продвинутых. Формула эта интересна тем, что в пределе

Разве это не удивительно?
Разве это не удивительно?
Последний раз редактировалось Георгий 30 ноя 2019, 08:08, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 4 гостей