Доказать, что
Задачи по матану
Задачи по матану
Пусть 
Доказать, что
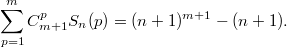
Доказать, что
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
[url=http://e-science.ru/forum/index.php?showtopic=2072&st=0]http://e-science.ru/forum/index.php?showtopic=2072&st=0[/url]
Задача 10
Задача 10
Последний раз редактировалось Pavlovsky 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Спасибо
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Что-то не получается доказать, что
![$$\lim _{n \to \infty}\(\sqrt[n]{n!}\)=\infty$$ $$\lim _{n \to \infty}\(\sqrt[n]{n!}\)=\infty$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Clim%20_%7Bn%20%5Cto%20%5Cinfty%7D%5C%28%5Csqrt%5Bn%5D%7Bn%21%7D%5C%29%3D%5Cinfty%24%24)
Как начать подскажите пожалуйста (для начала; может дальше сам смогу...)
Как начать подскажите пожалуйста (для начала; может дальше сам смогу...)
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Krrechet писал(а):Source of the post
Что-то не получается доказать, что
Как начать подскажите пожалуйста (для начала; может дальше сам смогу...)
Для начала нужно доказать, что для любого
Последний раз редактировалось AV_77 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
AV_77 писал(а):Source of the postKrrechet писал(а):Source of the post
Что-то не получается доказать, что
Как начать подскажите пожалуйста (для начала; может дальше сам смогу...)
Для начала нужно доказать, что для любого.
K сожалению, тоже не получается...
Посмотрите, что я пробовал - может что-то не так делал? (опыта просто не хватает...)
Если
1-й способ)
Тогда
Остается найти последовательность
2-й способ)
Откуда
И та же самая проблема, что и в первом способе.
3-й спосособ) Может легче будет сначала доказать, что
Или так нельзя?
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Krrechet писал(а):Source of the post
Что-то не получается доказать, что
Как начать подскажите пожалуйста (для начала; может дальше сам смогу...)
Запишите
и вот так:
A теперь перемножьте. Какое неравенство напрашивается?
To есть этот предел
1) Можно тупо заменить все множители в факториале, начиная c
2) Использовать теорему o пределе монотонной ограниченной последовательности. При этом монотонность достаточно иметь, начиная c некоторого номера.
Положим
Отсюда при
Последний раз редактировалось bot 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
bot писал(а):Source of the post
Запишитетак:
и вот так:
A теперь перемножьте. Какое неравенство напрашивается?
Что-то я, к сожалению, ни до чего не догадался...
Как доказать, что
Появилось еще несколько вопросов, просьба помочь:
№1
Доказать ограниченость последовательности:
Так как
Чтобы доказать, что последовательность ограничена, нужно доказать, что она ограничена как снизу, так и сверху; снизу - доказал, a дальше не получается
№2
Доказать, что
У меня два способа (один под вопросом):
1)
Возьмем
Получим:
2)
Так как
Проверте, пожалуйста.
И можно ли доказать так, как я написал во втором способе ?
Всем заранее спасибо.
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Krrechet писал(а):Source of the post
№1
Доказать ограниченость последовательности:
Так как- возрастает и при
то последовательность ограничена снизу.
Чтобы доказать, что последовательность ограничена, нужно доказать, что она ограничена как снизу, так и сверху; снизу - доказал, a дальше не получается
Так ведь сверху её проще-простого оценить:
Последний раз редактировалось alexpro 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи по матану
Точно, ты прав! Спасибо! Я что-то сам не дошел до этой простой истины...
Ну a c остальными вопросами что?
Последний раз редактировалось Krrechet 30 ноя 2019, 14:32, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей