Условный экстремум, метод множителей Лагранжа.Mihail-Nor писал(а):Source of the post Хотелось бы как-то оценить сверху эту функцию на произвольной окружности. Не понятно, как это можно сделать.
Предел функции двух переменных
Предел функции двух переменных
Последний раз редактировалось 12d3 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Предел функции двух переменных
Трудоемкость вычислений обычно сопутствует топорности метода.)Mihail-Nor писал(а):Source of the post Поиск точного максимума (приравнивание производной к нулю) приводит к очень сложному уравнению
Последний раз редактировалось 12d3 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
- Mihail-Nor
- Сообщений: 43
- Зарегистрирован: 14 сен 2012, 21:00
Предел функции двух переменных
Не понятно, как аналитически решать получающуюся систему уравнений метода Лагранжа.
Последний раз редактировалось Mihail-Nor 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Предел функции двух переменных
И действительно, чет непонятно, что с ней делать.
Последний раз редактировалось 12d3 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Предел функции двух переменных
Тут на графиках x/R обозначено как х
Максимум дроби стремится к 0 с ростом R, но уж очень медленно, примерно как lnR
Пробовал разные a и b, так всегда
Надо использовать то, что порядок роста знаменателя, при R большом, больше чем числителя.Например, такая лемма.

Ну и значит, дробь не больше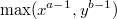 , эта оценка не стремится к 0 только если х или у вообще не стремятся к бесконечности. Но если одно из них ограничено, то дробь оценить еще проще.
, эта оценка не стремится к 0 только если х или у вообще не стремятся к бесконечности. Но если одно из них ограничено, то дробь оценить еще проще.
Можно увеличить строгость этого рассуждения. a,b фиксированы. Для каждого R найдем точку максимума дроби на окружности x®,y®-в 1м квадранте ищем, должна быть одна. Она должна бы непрерывно зависеть от R. получаем кривую, удаляющуюся от 0, по которой дробь только и нужно смотреть.И вот тут уже можно говорить, стремится ли к бесконечности х отдельно или нет.Вряд ли х на этой кривой бесконечно колеблется. Но это все еще не строго
Гельдер - просто подобрать не удается.Там же огрублять можно некоторые слагаемые, а также есть неравенства для степенных средних.Зато когда подберется, выйдет решение в одну строчку

Максимум дроби стремится к 0 с ростом R, но уж очень медленно, примерно как lnR
Пробовал разные a и b, так всегда
Надо использовать то, что порядок роста знаменателя, при R большом, больше чем числителя.Например, такая лемма.
Ну и значит, дробь не больше
Можно увеличить строгость этого рассуждения. a,b фиксированы. Для каждого R найдем точку максимума дроби на окружности x®,y®-в 1м квадранте ищем, должна быть одна. Она должна бы непрерывно зависеть от R. получаем кривую, удаляющуюся от 0, по которой дробь только и нужно смотреть.И вот тут уже можно говорить, стремится ли к бесконечности х отдельно или нет.Вряд ли х на этой кривой бесконечно колеблется. Но это все еще не строго
Гельдер - просто подобрать не удается.Там же огрублять можно некоторые слагаемые, а также есть неравенства для степенных средних.Зато когда подберется, выйдет решение в одну строчку
Последний раз редактировалось Ian 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
- Mihail-Nor
- Сообщений: 43
- Зарегистрирован: 14 сен 2012, 21:00
Предел функции двух переменных
Да, при 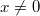 и
и  есть оценка
есть оценка

но нужны ещё другие оценки, если x или y близки к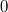 . Если из таких трёх оценок удастся склеить одну, стремящуюся к нулю при
. Если из таких трёх оценок удастся склеить одну, стремящуюся к нулю при  , то утверждение будет доказано. Пока такие оценки получить не удаётся.
, то утверждение будет доказано. Пока такие оценки получить не удаётся.

но нужны ещё другие оценки, если x или y близки к
Вот график координат этой точки. Но, к сожалению, их строго оценить не получается.Ian писал(а):Source of the post Для каждого R найдем точку максимума дроби на окружности
Если вообще что-то подберётся. Не понятно же, как и что подбирать, чтобы исходную дробь оценить так, чтобы можно было сделать вывод о стремлении к нулю.Ian писал(а):Source of the post Зато когда подберется, выйдет решение в одну строчку

Последний раз редактировалось Mihail-Nor 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Предел функции двух переменных
Вы знаете, это не самое сложное, что есть в матане. В теории асимптотических рядов такой прием в каждой теореме.Mihail-Nor писал(а):Source of the post Да, прии
есть оценка
но нужны ещё другие оценки, если x или y близки к. Если из таких трёх оценок удастся склеить одну, стремящуюся к нулю при
, то утверждение будет доказано. Пока такие оценки получить не удаётся.
Пусть для определенности
1) Если пороговое неравенство выполняется, то х стремится к бесконечности при R стремящемся к бесконечности.
2)Если выполняется неравенство. противоположное пороговому, то у стремится к бесконечности при R стремящемся к бесконечности.
Значит, достаточно взять
Последний раз редактировалось Ian 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
- Mihail-Nor
- Сообщений: 43
- Зарегистрирован: 14 сен 2012, 21:00
Предел функции двух переменных
Вот это работает, утверждение доказано.
Причём для этого рассуждения даже не требуется предположение .
.
Спасибо!
Причём для этого рассуждения даже не требуется предположение
Спасибо!
Последний раз редактировалось Mihail-Nor 27 ноя 2019, 19:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 5 гостей