Решить функциональное уравнение

geh · Сообщение **geh** » 26 дек 2013, 14:38

Решить следующее уравнение
$\underbrace{f(f( ... f}_{n}(x) ...)=x^2$
запишем это коротко, например так:
$$F_nf(x)=x^2$$

далее я сделал предположение, что искомая функция
является степенной, то есть $f(x)=x^{\alpha}$
отсюда следует, что
$F_nx^{\alpha}=x^{\alpha^n}$
решая уравнение $x^{\alpha^n}=x^2$ получим, что
$\alpha=\sqrt[n]{2}$ и далее
$f(x)=x^{\sqrt[n]{2}}$
итак я нашел одно решение, но могут быть и другие.
Это уравнение будет решено, если я найду все решения
либо докажу, что других решений нет.
Ни то, ни другое мне не подвластно. Может у кого есть на сей счет идея??
буду очень благодарен любой подсказке.

Ian · Сообщение **Ian** » 26 дек 2013, 19:25

geh писал(а):Source of the post
$f(x)=x^{\sqrt[n]{2}}$

Точнее $\displaystyle f(x)=|x|^{\sqrt[n]{2}}$
Как это еще проще написать взятие такой функции
Берется $\ln |x|$ (или по другому основанию, если оч.хочется)
Записывается двоичной дробью $$x_0,x_1x_2....$$

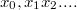
(до запятой может быть и больше знаков, но это неважно.пусть мы решаем уравнение только для $$|x|<e^2$$

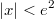
, разница невелика)
Берется ${\sqrt[n]{2}}$
Записывается в двоичной системе 1,0...(установите закономерность)
Оказывается, n-кратное умножение на ${\sqrt[n]{2}}$ равносильно сдвигу любой последовательности нулей и единиц $$x_0,x_1x_2....$$

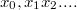
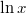
на один символ влево .(так как $\ln x$ должен умножиться на 2) Но только ли преобразование умножения на ${\sqrt[n]{2}}$ обладает таким свойством? вряд ли, можно чего -нибудь настроить с перетасовкой этих нулей и 1ц даже без сложения (напоминаю, что умножение это многократное сложение с собой со сдвигом разрядов). Это даст не непрерывные решения исходного уравнения.
А непрерывное, видимо, только это. Общая схема работы с функурами, в которых, кроме неизвестной функции, есть умножение, но нет сложения:
Заменяем неизвестную функцию $f=\exp \circ g \circ \ln$ ,тогда, в частности, Ваше уравнение запишется в виде $\exp\circ g\circ \ln \circ (\exp \circ g\circ \ln \circ ...)g \circ \ln x=x^2$
(с оговорками про изменение области определения)
$g^n(\ln x)=2\ln x$
$$g^n (t)=2t$$

, его-то решать попроще, и доказать что других непрерывных решений нет- реально

zykov · Сообщение **zykov** » 26 дек 2013, 19:50

Ian писал(а):Source of the post $\displaystyle f(x)=|x|^{\sqrt[n]{2}}$

Для чётных n так же подходит $\displaystyle f(x)=|x|^{-\sqrt[n]{2}}$ .

geh · Сообщение **geh** » 27 дек 2013, 06:05

Большое спасибо! Я вам так благодарен.
Такие уравнения столь редко встречаются, что
нет никакого опыта в их решении. Еще раз большое спасибо!!

Ian · Сообщение **Ian** » 27 дек 2013, 08:21

Ian писал(а):Source of the post можно чего -нибудь настроить с перетасовкой этих нулей и 1ц...

Как водится, любой теоретический материал должен завершаться каким-нибудь тестиком для самопроверки

Сколько решений имеет функциональное уравнение $$f(f(f(x)))=x$$

среди функций, определенных для всех действительных х ?
0)ни одного
1)одно
2)два
3)бесконечно много

zykov · Сообщение **zykov** » 27 дек 2013, 21:44

Ian писал(а):Source of the post Сколько решений имеет функциональное уравнение среди функций, определенных для всех действительных х ?

Можно взять 3 любых интервала (например от минус бесконечности до 0, от 0 до 1 и от 1 до плюс бесконечности) и взять любую обратимую функкцию из первого интервала во второй и из второго в третий. А из третьего в первый взять обратную к композиции этих двух. Для 0 и 1 функция переводит их в себя.
(По мне так проще, чем с бесконечными дробями.)

Здесь несколько проще, чем с квадратом, поскольку тройная композиция переводит любоe множество в себя.

yourdomain.com