laplas писал(а):Source of the post я не понимаю. вы меня запутали.
какое преобразование экспонент из двух верное?
я второй день пытаюсь получить ваше выражение, все бестолку.
Там точно
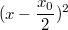
при выделении полного квадрата, а у вас этого нет. Но это просто упражнение, никак не применяемое при решении поставленной задачи
может тогда просто взять и руками взять несколько интегралов, сначала
n=m=0,1,2,
а потом для n не равных m?
хотя я не уверен, что интегралы для n и m больше нуля будут браться.
Будут!! В уме!! Ради того я и пост писал. Это же хорошая идея Эрмита &Co: ортогональные многочлены со степенями, возрастающими через 1, не просто ортогональны друг другу, а каждый
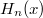
ортогонален всем многочленам степени строго ниже n. Доказательство .Пусть
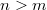
,
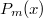
произвольный степени m. Разложим
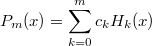
, это можно сделать делением с остатком
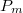
на
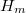
, остаток многочлен степени не выше
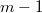
, его разделим с остатком на
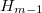
и т.д. Теперь
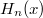
ортогонален всем упомянутым
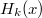
, а значит, их линейной комбинации.
Поэтому от
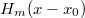
мы используем только то, что его степень m, а не то, что он сдвинутый эрмитов.Ответ: интегралы в посте 1 равны 0 при

Наконец, что делать при

- рассмотреть
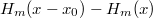
, его степень ровно m-1 и он уже ортогонален