Интегрирование
Интегрирование
Скажите пожалуйста, где можно (лучше в интернете) найти доказательство того, что интеграл Лебега-Стилтьеса (и Риманна-Стилтьеса) могут быть построены только когда интегрируем по функции имеющей ограниченную вариацию?
Последний раз редактировалось Math 28 ноя 2019, 07:07, всего редактировалось 1 раз.
Причина: test
Причина: test
Интегрирование
Некоторые авторы предполагают уже при определении каждого из этих интегралов, что функция имеет ограниченную вариацию, например известная Вам книга Колмогоров-Фомин , а некоторые нет (вот например такая ссылка на пдф, пример 4). И как вы представляете себе доказательство того, что f интегрируема по g ТОЛЬКО если g=ОВ? Что интегральные суммы расходятся ? Но для f=0 они всегда равны 0.
Последний раз редактировалось Ian 28 ноя 2019, 07:07, всего редактировалось 1 раз.
Причина: test
Причина: test
Интегрирование
Мой вопрос возник из того, что стохастический интеграл (интеграл Ито по Броуновскому движению) нельзя строить как интеграл Риманна-Стилтьеса (то есть делать потраекторное интегрирование) потому что Броуновское движение имеет неограниченную вариацию. Здесь говорится, что имеется доказательство того, что если интеграл  существует как интеграл Риманна-Стилтьеса для всех непрерывных
существует как интеграл Риманна-Стилтьеса для всех непрерывных 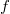 на
на ![$$[0,1]$$ $$[0,1]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5B0%2C1%5D%24%24) , то
, то 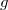 должна быть обязательно ограниченной вариации.
должна быть обязательно ограниченной вариации.
Последний раз редактировалось Math 28 ноя 2019, 07:07, всего редактировалось 1 раз.
Причина: test
Причина: test
Интегрирование
Для всех непрерывных f- тогда это реально. Но должны быть предварительные условия и на g, хватит кусочной непрерывности и почти всюду дифференцируемости.Тогда доказать можно по такой схеме:Math писал(а):Source of the post Здесь говорится, что имеется доказательство того, что если интегралсуществует как интеграл Риманна-Стилтьеса для всех непрерывных
на
, то
должна быть обязательно ограниченной вариации.
Однако броуновские траектории, кажется, нигде не дифференцируемы с верояностью 1
А про интеграл Ито я не в курсе. если бы где-то это было аккуратно определено, интересно почитать)
Последний раз редактировалось Ian 28 ноя 2019, 07:07, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 11 гостей