Асимптотика сумм с дробной частью

JeffLebovski

Для примера: $\sum\limits_{k=1}^{n}\{\ln k\}=\frac{n}{2}+o(n)$ . Подскажите, как найти второй член асимптотического разложения?

Sonic86 · Сообщение **Sonic86** » 05 авг 2012, 05:08

Находите в лоб: $\{t\}=t-[t]$ , а суммы с целой частью часто могут быть хорошо оценены:
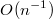$\{\ln k\}=\ln k - [\ln k]$ , суммируете - 1-е слагаемое = $\ln n!$ , а его асимптотика известна до какого угодно члена (уже формула Стирлинга дает ее с точностью $O(n^{-1})$ ). Остается 2-я сумма. Предлагаю Вам ее самому помучить - разбить на несколько сумм с одинаковым значением $[\ln k]$ . Я пока тоже сам попробую :oops:

P.S. Если есть какое-то решение в рамках теории равномерного распределения - от меня его не ждите, я его не знаю.

upd1: попробовал - получается какая-то ересь, даже $n\ln n$ не сократился
Еще идея - попробовать формулу Эйлера-Маклорена.

upd2: Эмпирически $-C_1\ln n\leqslant\sum\limits_{k=1}^n\{\ln k\}-\frac{n}{2}\leqslant C_2\ln n$ , причем $C_1\leqslant C_2 \leqslant \frac{3}{4}$

upd3: Пересчитал получше, получилось $\sum\limits_{k=1}^n[\ln k] = n[\ln n]-e^{[\ln n]}\frac{e}{e-1}+O(\ln ^2n)$ , т.е. $n\ln n$ уже правильно выходит, а коэффициент перед $$n$$

не получается? Никто пересчитать не может нормально? Кстати, это и есть $\int\limits_1^n [\ln x]dx$ , приближающий сумму примерно с той же точностью.

Ian · Сообщение **Ian** » 06 авг 2012, 05:51

JeffLebovski писал(а):Source of the post
Для примера: $\sum\limits_{k=1}^{n}\{\ln k\}=\frac{n}{2}+o(n)$ .

А где это опубликовано? Мне кажется, что $\sum\limits_{k=1}^{n}\{\ln k\}=\frac{n}{e-1}+o(n)$ , хотя не досчитал еще. $\frac 1{e-1}$ это интегральное среднее $\ln x$ по отрезку от 1 до е.
UPD: Это я по подпоследовательности $$n=[e^m]$$

считал. А вообще отношение этой суммы к n не имеет предела, осциллирует. По подпоследовательности $n=[e^{m+0,5}]$ предел даже меньше 0,5

Sonic86 · Сообщение **Sonic86** » 06 авг 2012, 10:13

Блин, а я вчера подумал, что я считать разучился... Эмпирика меня подвела, $e-1 \approx 2$ , блин, (много ругани шепотом...)

JeffLebovski

Ian, да это я прокололся когда считал. Я случайно доказал ррмод1 $\ln n,n=1,2,\ldots$ , что не верно.

yourdomain.com