Доказать тождество
Доказать тождество
Как можно доказать такое тождество?

Последний раз редактировалось Vector 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Какие ограничения на  ? Скажем, для
? Скажем, для 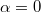 и
и 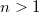 равенство не выполняется.
равенство не выполняется.
Последний раз редактировалось fri739 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Ещё. Левая часть непрерывна при любых  , а правая нет. При n=2 равенство не выполняется ни при каком
, а правая нет. При n=2 равенство не выполняется ни при каком 
Последний раз редактировалось bot 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
bot писал(а):Source of the post
Ещё. Левая часть непрерывна при любых, а правая нет. При n=2 равенство не выполняется ни при каком
Прошу прощения, пропустил сомножитель
Последний раз редактировалось Vector 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Не спасает. Найдутся такие  , при которых
, при которых
Возьмём , например
, например 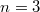 и рассмотрим предел левой и правой части при
и рассмотрим предел левой и правой части при  . Левый существует, а правый нет.
. Левый существует, а правый нет.
Возьмём
Последний раз редактировалось bot 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
А вообще, если там действительно есть верное соотношение, то это 2 дробно-рациональные функции. Можно их рассмотреть от переменной  : каждая дробно-рациональная функция определяется множеством нулей и полюсов (с кратностями) и константой. Находим нули и полюсы выражения слева и справа (можно предварительно упростить) и находим константы и сравниваем.
: каждая дробно-рациональная функция определяется множеством нулей и полюсов (с кратностями) и константой. Находим нули и полюсы выражения слева и справа (можно предварительно упростить) и находим константы и сравниваем.
Последний раз редактировалось Sonic86 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
через комплексные числа записал, может, поможет
Последний раз редактировалось Ian 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Левую часть можно рассматривать как интегральную сумму. Тогда переходя к пределу получим


При этот предел совпадает с пределом правой части, то есть в качестве приближённого равенства при больших n его рассматривать можно. Про конечное
этот предел совпадает с пределом правой части, то есть в качестве приближённого равенства при больших n его рассматривать можно. Про конечное  уже сказал.
уже сказал.
Проверяйте.
Upd. Исправил свой косяк со знаком.
При
Проверяйте.
Upd. Исправил свой косяк со знаком.
Последний раз редактировалось bot 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Хм, а ведь прощёлкал - в
Последний раз редактировалось bot 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать тождество
Сумма, похожа на обратное ДПФ.
Последний раз редактировалось Vector 28 ноя 2019, 17:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей