yourdomain.com

Вычислить сумму $1 + \sum\limits_{k=1}^{n}{C_n^k}\cos k\alpha$

RK05 писал(а):Source of the post
Вычислить сумму $1 + \sum\limits_{k=1}^{n}{C_n^k}\cos k\alpha$

По-моему, достаточно вспомнить, что $\cos k\alpha + i\sin k\alpha = e^{ik\alpha}$ ?

kiv писал(а):Source of the post
RK05 писал(а):Source of the post
Вычислить сумму $1 + \sum\limits_{k=1}^{n}{C_n^k}\cos k\alpha$

По-моему, достаточно вспомнить, что $\cos k\alpha + i\sin k\alpha = e^{ik\alpha}$ ?

Я понятия не имею что вы написали. Пожалуйста объясните что это такое, а то я уже мучаюсь из-за этой задачи.

RK05 писал(а):Source of the post
Вычислить сумму $1 + \sum\limits_{k=1}^{n}{C_n^k}\cos k\alpha$

Попробуйте использовать формулу Муавра [url=http://ru.wikipedia.org/wiki/%D4%EE%F0%EC%...%F3%E0%E2%F0%E0]http://ru.wikipedia.org/wiki/%D4%EE%F0%EC%...%F3%E0%E2%F0%E0[/url]

RK05 писал(а):Source of the post
Я понятия не имею что вы написали. Пожалуйста объясните что это такое, а то я уже мучаюсь из-за этой задачи.

Да нет, это вроде бы не особо упрощает... Или я не знаю, как упростить

Моя идея была -
$(1+e^{i\alpha})^n=1+\sum_{k=1}^{n}{C_n^k\cos k\alpha} +i\sum_{k=1}^{n}{C_n^k\sin k\alpha}$

но что-то не соображу, что дальше...

Да... Я вообще далек от того, что вы написали.

Ну так изучайте - Вам уже практически всё выложили.

kiv писал(а):Source of the post
но что-то не соображу, что дальше...

Дальше формула Муавра - ведь основание в левой части легко представимо в тригонометрической форме.

Комплексные числа тут сами напрашиваются. Без них нормального решения может вообще не быть.
Откуда задача взята?

bot писал(а):Source of the post
kiv писал(а):Source of the post
но что-то не соображу, что дальше...

Дальше формула Муавра - ведь основание в левой части легко представимо в тригонометрической форме.

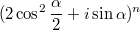
Не, не соображу никак. Ну имеем $(1+\cos\alpha + i\sin\alpha)^n$ . Ну или $(2\cos^2\frac{\alpha}{2}+i\sin\alpha)^n$ ... И что это нам дает? Если расписывать через биномиальные коэффициенты - получим что-то длинное и неудобозаписываемое...

Причем чувствую, что что-то очень простое, и - никак...

kiv писал(а):Source of the post
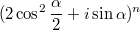
Не, не соображу никак. Ну имеем $(1+\cos\alpha + i\sin\alpha)^n$ . Ну или $(2\cos^2\frac{\alpha}{2}+i\sin\alpha)^n$ ... И что это нам дает? Если расписывать через биномиальные коэффициенты - получим что-то длинное и неудобозаписываемое...

Дальше возвелите в степень по формуле Муавра, но сначала комплексное число слева запишите в тригонометрической виде.

yourdomain.com

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика

Комбинаторика