разбор тезисов из методички заочника матфака
Добавлено: 04 янв 2012, 12:43
Вопрос
1) Тезис ниже (оформленный цитатой). Зачем оправдывать выбор обозначения и каким образом утверждение здесь оправдано?
2) Какие материалы полезно посмотреть еще?
Вместо лирического вступления
В методичке по дисциплине "Линейная алгебра и геометрия" (Многомерные пространства) на заочном отделении математического факультета есть множество утверждений, которые
в силу жанра не совсем ясны рядовому студенту. Пробовал разбираться сам, вместе с однокурсниками, мучил вопросами автора. Но из-за работы к автору на набегаешься. Вот
поэтому вынужден просить помощи здесь (на специализированном форуме). Уже когда писал это сообщение стало что-то проясняться в сознании. Но хотелось бы получить некий
аналог обратной связи, чтобы убедиться в правильности своего восприятия в частном вопросе и быть может найти более постоянную помощь. Мне не нужно просто решение
задач, хотелось бы, чтобы что-то осталось в голове... но и баланс найти важно. Сейчас цель получить документ об образовании стоит достаточно остро... а вот хвостов
накопилось В моем случае хвосты появляются в том числе из-за того, что "зарываюсь" в материал, при этом реально нет возможности столько времени расходовать на
учебу. Все подробности могу сообщить в личной переписке.
Аффинная система координат и формулы перехода
Определение 1.
Аффинной системой координат (в дальнейшем АСК) в называется упорядоченный набор точек
называется упорядоченный набор точек  , ...
, ...  , таких, что
, таких, что  образуют векторный базис пространства переносов
образуют векторный базис пространства переносов 
Иначе, АСК - это набор из одной точки (начало АСК) и векторного базиса
(начало АСК) и векторного базиса  , ...
, ... 
Определение 2.
Координатами точки M относительно АСК {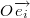 } называются координаты ее радиус-вектора
} называются координаты ее радиус-вектора 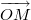 относительно
относительно
векторного базиса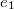 , ...
, ... 
Здесь и далее договоримся координаты обозначать буквами с индексами наверху, причем в любом выражении, содержащем индекс один раз вверху и один раз внизу, производить
суммирование по этому индексу от 1 до n. Тогда из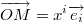 следует, что координаты точки
следует, что координаты точки 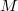 будут числа
будут числа
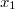 , ...
, ... 
Предложение.
Пусть в АСК координаты точек
координаты точек 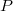 и
и 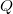 будут соответственно,
будут соответственно, 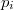 и
и 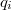 . Тогда
. Тогда
координатами вектора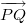 служат числа
служат числа 
Доказательство
В самом деле, если , то это значит, что
, то это значит, что  . тогда
. тогда 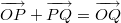 , откуда следует, что
, откуда следует, что 
1) Тезис ниже (оформленный цитатой). Зачем оправдывать выбор обозначения и каким образом утверждение здесь оправдано?
2) Какие материалы полезно посмотреть еще?
Вместо лирического вступления
В методичке по дисциплине "Линейная алгебра и геометрия" (Многомерные пространства) на заочном отделении математического факультета есть множество утверждений, которые
в силу жанра не совсем ясны рядовому студенту. Пробовал разбираться сам, вместе с однокурсниками, мучил вопросами автора. Но из-за работы к автору на набегаешься. Вот
поэтому вынужден просить помощи здесь (на специализированном форуме). Уже когда писал это сообщение стало что-то проясняться в сознании. Но хотелось бы получить некий
аналог обратной связи, чтобы убедиться в правильности своего восприятия в частном вопросе и быть может найти более постоянную помощь. Мне не нужно просто решение
задач, хотелось бы, чтобы что-то осталось в голове... но и баланс найти важно. Сейчас цель получить документ об образовании стоит достаточно остро... а вот хвостов
накопилось В моем случае хвосты появляются в том числе из-за того, что "зарываюсь" в материал, при этом реально нет возможности столько времени расходовать на
учебу. Все подробности могу сообщить в личной переписке.
Аффинная система координат и формулы перехода
Определение 1.
Аффинной системой координат (в дальнейшем АСК) в
Иначе, АСК - это набор из одной точки
Определение 2.
Координатами точки M относительно АСК {
векторного базиса
Здесь и далее договоримся координаты обозначать буквами с индексами наверху, причем в любом выражении, содержащем индекс один раз вверху и один раз внизу, производить
суммирование по этому индексу от 1 до n. Тогда из
Предложение.
Пусть в АСК
координатами вектора
Доказательство
В самом деле, если
Заметим, что если, то точка
имеет координаты
, что
оправдывает выбор обозначения