Линейная алгебра
Добавлено: 27 авг 2011, 16:29
Пусть
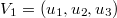 (линейная оболочка строк
(линейная оболочка строк 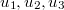 ) ,
) ,
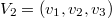 (линейная оболочка строк
(линейная оболочка строк 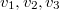 ) ,
) ,
Найти базисы линейных пространств
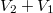
и

при этом строки
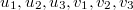
выразить через базис пространства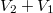
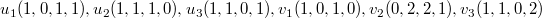
Решение:
Решение не должно быть не сложным я думаю, но я просто ни разу подобных задач не свтречала. Думаю надо составить системы уравнений, определяющие оболочки...

Тут матрицу к диагональному виду вроде привести, но как получаются уравнения с а, не понимаю, помогите пожалуйста.
Найти базисы линейных пространств
и
при этом строки
выразить через базис пространства
Решение:
Решение не должно быть не сложным я думаю, но я просто ни разу подобных задач не свтречала. Думаю надо составить системы уравнений, определяющие оболочки...
Тут матрицу к диагональному виду вроде привести, но как получаются уравнения с а, не понимаю, помогите пожалуйста.