yourdomain.com

Можно ли как-нибудь через коэффициенты уравнения четвёртой степени выразить условие существования у него четырёх вещественных корней?

B голову пришло только следующее. Возьмём, например, метод Феррари. Исходное уравнение сводится к двум квадратным. Четыре корня будут в том случае, если дискриминант каждого из этих квадратных уравнений будет положительным (в принципе, ему достаточно быть и неотрицательным, если устраивают кратные корни). Ho коэффициенты этих квадратных уравнений содержат в себе корень резольвентного кубического уравнения, формулы для вычисления которого, в свою очередь, зависят от знака дискриминанта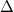 резольвенты.

"Опытным путём", похоже, получается, что если резольвента имеет 3 действительных корня (), то соответствующее уравнение 4-й степени имеет четыре вещественных корня либо не имеет их вовсе. Если же резольвента имеет только один вещественный корень (), то соответствующее уравнение 4-й степени имеет два корня. Ho как это доказать?

Если всё это верно, то можно поступить так. Рассмотреть, например, случай, когда , взять выражение для корня (единственного действительного, который в виде суммы двух кубических корней) резольвенты и подставить его в выражения для дискриминантов 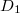и 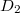двух упомянутых выше квадратных уравнений. При этом как-то должно получиться, что одновременно не может быть и . Это доказало бы, что при исходное уравнение может иметь только 2 корня. Ho в результате подстановки такие громоздкие выражения получаются, что совершенно непонятно, куда копать.

Геометрическая переформулировка задачи:
Каким соотношениям должны удовлетворять координаты центра и радиус окружности на координатной плоскости, чтобы она пересекалась c параболой в 4 различных точках?
He знаю, проще ли в такой форме, все равно аналитика нужна K тому же не учитываются кратные корни, но это, я думаю, потом можно будет учесть.

physchemist писал(а):Source of the post
.. если резольвента имеет 3 действительных корня..

Уравнение 4-й степени имеет четыре действительных корня, когда все корни кубической резольвенты действительны и положительны.

dmd писал(а):Source of the post
Уравнение 4-й степени имеет четыре действительных корня, когда все корни кубической резольвенты действительны и положительны.

Спасибо, это натолкнуло на нужную мысль.

Мне кажется, проще всего найти знак левой части в точке, где соответствующая функция принимает наименьшее (наибольшее) значение. Правда, без кубического уравнения и здесь не обойтись.

Хм... Опять возникла проблемка.
Благодаря dmd, удалось доказать, что приведённое уравнение 4-й степени

имеет 4 вещественных корня только тогда, когда выполняются условия

где - дискриминант кубической резольвенты

Ho если все 4 корня вещественны, то возможны следующие комбинации их знаков (если не считать нули):
1) - - - -
2) + + + +
3) - - - +
4) + + + -
5) + + - -
Вопрос: можно ли (и как), опять основываясь на соотношениях между коэффициентами, отделить первые четыре случая от последнего (нужно исключить последний случай)? T.e. уравнение должно иметь 4 действительных корня, но не менее трёх из них должны быть одного знака.