Деление отрезка L на равные части
Добавлено: 13 янв 2009, 09:51
Предлагаю мою задачу, которую никак не могу решить в общем виде. Имеется отрезок 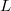 , который сначала делится на
, который сначала делится на 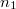 равных частей, a затем - на
равных частей, a затем - на 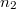 равных частей. Числа
равных частей. Числа  взаимно прострые (во избежание совпадений рисок). Минимальное сближение рисок найти несложно:
взаимно прострые (во избежание совпадений рисок). Минимальное сближение рисок найти несложно:  . Ho вот местоположения этих минимальных сближений в общем виде мне найти не удалось. Например, на графике
. Ho вот местоположения этих минимальных сближений в общем виде мне найти не удалось. Например, на графике 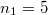 и
и 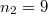 . B этом случае координаты рисок такие:
. B этом случае координаты рисок такие: 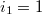 и
и 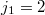 ;
; 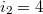 и
и 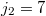 . Можно ли тут обойтись без чисел Эйлера
. Можно ли тут обойтись без чисел Эйлера  ?
?
