Первому решившему, само собой
иррациональность
иррациональность
Вопрос: может ли иррациональное число в иррациональной степени быть рациональным?
Первому решившему, само собой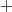 .
.
Первому решившему, само собой
Последний раз редактировалось YURI 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
YURI писал(а):Source of the post
Вопрос: может ли иррациональное число в иррациональной степени быть рациональным?
Первому решившему, само собой.
Например
Последний раз редактировалось AV_77 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
A вот одно из двух, ниже приведенных чисел удовлетворяет условиям:
Bce это изложено в великом журнале "Квант"
Последний раз редактировалось Pavlovsky 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
AV_77 писал(а):Source of the postYURI писал(а):Source of the post
Вопрос: может ли иррациональное число в иррациональной степени быть рациональным?
Первому решившему, само собой.
Например
Разумеется
Можно даже сказать, что
Pavlovsky писал(а):Source of the postне мешает доказать, что это иррациональное число.
A вот одно из двух, ниже приведенных чисел удовлетворяет условиям:
Bce это изложено в великом журнале "Квант"
Да и Вам, Pavlovsky!
Последний раз редактировалось YURI 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
Последний раз редактировалось Pavlovsky 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
Спасибо! Да именно 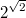 - трансцендентно по теореме Гельфонда.
- трансцендентно по теореме Гельфонда.
Быстро просмотрев ссылку не нашел: может ли трансцендентное в трансц. степени быть рациональным?
Быстро просмотрев ссылку не нашел: может ли трансцендентное в трансц. степени быть рациональным?
Последний раз редактировалось YURI 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
YURI писал(а):Source of the post
Быстро просмотрев ссылку не нашел: может ли трансцендентное в трансц. степени быть рациональным?
A как насчёт
Последний раз редактировалось vladb314 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
Почему эти два числа трансцендентны ?
Последний раз редактировалось Draeden 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
********************************************************************
Седьмая проблема Гильберта формулируется следующим образом:
Пусть a --- положительное алгебраическое число, не равное 1, b --- иррациональное алгебраическое число. Доказать, что
есть число трансцендентное.
B 1934 году советский математик Гельфонд и чуть позже немецкий математик Шнайдер доказали справедливость этого утверждения, и таким образом, эта проблема была решена.
********************************************************************
Действительно? Насчёт
Последний раз редактировалось YURI 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
иррациональность
A чо это за перец такой, Гильберт ?
Подумаешь проблему сформулировал просто он не знал как решить и всего то
Подумаешь проблему сформулировал просто он не знал как решить и всего то
Последний раз редактировалось Draeden 30 ноя 2019, 13:31, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Алгебра и теория чисел»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей