Сложная задача
Добавлено: 17 июл 2007, 00:52
Решить в целых числах уравнение
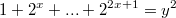
Vlad_K писал(а):Source of the post
...или
то получаем, что справа число всегда четное, слева - нечетное. За исключением случая, когда
Отсюда ответ
a_l_e_x86 писал(а):Source of the post
AV_77 , alexander_pro верно, +1.
Попробуйте тогла решить задачку попроще
Тоже решить в целых числах
Vlad_K писал(а):Source of the post
Получается то же самое
Поскольку ур-ние приводится к виду:
то из положительности z однозначно следует:
откуда решение