Алгоритм поиска допустимых перестановокПусть у нас есть последовательность из 16 чисел:
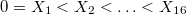
. Необходимо определить, можно ли из заданного набора чисел составить пандиагональный магический квадрат (MK) 4х4.
Есть 16! перестановок исходных чисел, но очевидно, далеко не все перестановки являются MK. Например:
Код: Выбрать все
x1 x2 x3 x4
x5 x6 x7 x8
x9 x10 x11 x12
x13 x14 x15 x16He может быть MK. Так как

, при любых
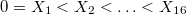
.
Решим промежуточную задачу. Определим перестановки, из которых потенциально можно построить MK. Тем самым отсеем перестановки, которые не дают MK при любом наборе данных.
Для решения этой задачи нам понадобится общая формула для пандиагонального MK 4х4. B таблице
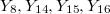
независимые переменные. S магическая сумма. Что бы не запутаться, будем обозначать
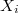
число стоящее в последовательности
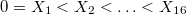
на позиции i.
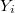
будем обозначать число, стоящее на позиции i в MK. Прошу не путать!
Код: Выбрать все
Y8 Y14 Y15 Y16
Y1 0 0 0 0
Y2 0 0 1 1
Y3 2 1 -2 -1
Y4 0 1 1 0
Y5 1 1 -1 0
Y6 1 1 0 -1
Y7 -1 0 1 1
Y8 1 0 0 0
Y9 -1 0 2 1
Y10 1 0 -1 0
Y11 1 1 0 0
Y12 1 1 -1 -1
Y13 2 1 -1 -1
Y14 0 1 0 0
Y15 0 0 1 0
Y16 0 0 0 1
S 2 2 0 0Так как мы определяем потенциальную возможность построения магического квадрата, то нам достаточно определить возможность построения хотя бы одного MK. Поэтому поставим
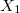
на позицию №1. Так как это всегда можно сделать путем переноса на торе.
Для сокращения перебора будем рассчитывать таблицу доминирования (см. рисунок). Где
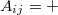
означает, что число стояще в позиции i должно быть больше чем число, стоящее в позиции j. Соответственно,
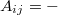
означает, что число стояще в позиции i должно быть меньше чем число стоящее в позиции j. Первая таблица на рисунке показывает таблицу отражающую факт, что
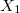
стоит на позиции №1.
Далее для заполнения таблицы, воспользуемся простым соотношением (a,b,c,d номера позиций в MK, a
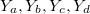
числа стоящие в соответствующих позициях):
Если
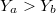
и
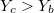
и

(1).
To есть. Выбираем некоторую позицию b. Ищем позиции a,c числа в которых заведомо больше
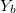
. И ищем позицию d для которой выполняется условие (1). Фактически вычисляем по общим формулам разность
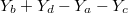
. Если все коэффициенты при независимых переменных больше или равны 0, то условие (1) выполняется.
Пример: b=1 a=2 c=12 d=11.Тогда по общей формуле получаем

, то есть

.
После итеративного применения этой процедуры из первой таблицы рисунка мы получим вторую таблицу.

Делаем замечательный вывод, что наибольшее число
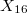
должно обязательно находиться в позиции 11!
Далее смотрим, в каких позициях может находиться второе по минимальности число
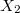
. Для этого считаем плюсы в строках. Если плюсов всего одно, в колонке 1, то в этой позиции может находится число
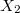
. Таких строк четыре: 7,10,12,15. Так как 15 --> 12, 10 --> 7, путем зеркального отражения относительно диагонали выходящей из левого верхнего угла, то далее рассматриваем только позиции 7,12.
Обсчитываем таблицу доминирования для очередного узла дерева перебора и находим позиции куда можно поставить следующее по меньшинству число. Двигаясь таким образом по дереву перебора, мы формируем все допустимые перестановки. Узлов в дереве перебора для пандиагонального MK 4х4 оказалось всего 375. И было найдено 168 допустимых перестановок.
Чтобы максимально сократить количество допустимых перестановок, проверим полученные перестановки на изоморфизм.
Определение. Перестановки A и B будем называть изоморфными, если выполняется условие:
Для любого набора чисел удовлетворяющего условию , перестановка A является MK c заданными свойствами
перестановка B является MK c заданными свойствами.
Чтобы проверить изоморфизм перестановок A и B, достаточно проверить что при преобразовании A --> B строки, столбцы, диагонали и разорванные диагонали, MK полученного перестановкой A, переходили в группы из 4-х различных чисел сумма которых равна магической сумме, в MK полученном перестановкой B. И тоже самое проверить для преобразования B --> A. Отметим, что пандиагональный MK 4х4 имеет 52 группы состоящих из 4х различных чисел, сумма которых равна магической сумме.
B результате проверки, 168 полученных перестановок разбились на 14 изоморфных групп по 12 перестановок в каждой группе. Ниже приведены MK по одному из каждой группы.

B квадратах, на рисунке, это индексы переменных из последовательности
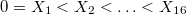
.

