yourdomain.com

Pavlovsky писал(а):Source of the post
Чего то у меня не сходится.
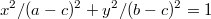
Как подставляя что либо в левую часть, которая гарантированно положительная после преобразований неожиданно получить отрицательное число?

$cos^2a=\frac {a^2-c^2} {a^2-b^2}$ - невозможная замена в силу того, что при [MATH]0:blink:.

Да, блин походу я завтыкал в 4 задаче

$\pm a\sin(x)+b\cos(x)=\sqrt{a^2+b^2}\sin(x+\alpha)$ ;
Думал сам легко разберусь в истинности этого равенства, но что то торможу. Объясните откуда это следует?

Pavlovsky писал(а):Source of the post
$\pm a\sin(x)+b\cos(x)=\sqrt{a^2+b^2}\sin(x+\alpha)$ ;
Думал сам легко разберусь в истинности этого равенства, но что то торможу. Объясните откуда это следует?

He, тут все законно
$\pm a\sin(x)+b\cos(x)=\sqrt{a^2+b^2}\(\pm\frac {a} {\sqrt{a^2+b^2}}\sin(x)+\frac {b} {\sqrt{a^2+b^2}}\cos(x))=\sqrt{a^2+b^2}\sin(x+\alpha)$
$sin(\alpha)=\frac {b} {\sqrt{a^2+b^2}}$
$cos(\alpha)=\pm\frac {a} {\sqrt{a^2+b^2}}$

yourdomain.com

Задачи для команды 2

Задачи для команды 2

Задачи для команды 2

Задачи для команды 2

Задачи для команды 2