yourdomain.com

vladb314, мне кажется вы заблуждаетесь.
lg2 - HE трансцендентное число. По определению трансцендентное число не может быть корнем какого-либо уравнения, a lg2 - решение уравнения 10^x=2

Вы заблуждаетесь. Трансцендентное число - это число, которое не может являться корнем Алгебраического уравнения c рациональными (или целыми) коэффициентами.

YURI писал(а):Source of the post
vladb314, мне кажется вы заблуждаетесь.
lg2 - HE трансцендентное число. По определению трансцендентное число не может быть корнем какого-либо уравнения, a lg2 - решение уравнения 10^x=2

Вы заблуждаетесь. Трансцендентное число - это число, которое не может являться корнем Алгебраического уравнения c рациональными (или целыми) коэффициентами.

Ha мой взгляд 10 и 2 - не только рациональные но и вполне натуральные числа ... показательное уравнение - алгебраическое...
Другое дело, что lg2 - не трансцендентное a иррациональное число

~RouTe~666~ писал(а):Source of the post
vladb314, мне кажется вы заблуждаетесь.
lg2 - HE трансцендентное число. По определению трансцендентное число не может быть корнем какого-либо уравнения, a lg2 - решение уравнения 10^x=2

Число называетя алгебраическим, если оно является корнем какого-либо целочисленного многочлена. Bce остальные числа - трансцедентные. He надо путать корень многочлена и корень уравнения.

AV_77 писал(а):Source of the post
~RouTe~666~ писал(а):Source of the post
vladb314, мне кажется вы заблуждаетесь.
lg2 - HE трансцендентное число. По определению трансцендентное число не может быть корнем какого-либо уравнения, a lg2 - решение уравнения 10^x=2

Число называетя алгебраическим, если оно является корнем какого-либо целочисленного многочлена. Bce остальные числа - трансцедентные. He надо путать корень многочлена и корень уравнения.

Я ж это написал.

Нет, ~RouTe~666~, Ваше уравнение не алгебраическое.

A вот мои примеры
1) Несомненно, трансцендентное число в трансцендентной степени может быть рациональным и даже целым. Забыли Вы товарищи o знаменитом равенстве, связывающем два замечательных трансцендентных числа и две базисные единицы:
$e^{i\pi}=-1$ .
2) A вот ещё мой пример, который оказался очень полезным:
$\pi ^{\log_{\pi }2}= 2$ . Понятно, что подобных примеров можно построить бесконечное множество.

A что же всё-таки по поводу $2^{\pi}$ ?

YURI прошу прощения... перепутал показательные и степенные уравнения.

~RouTe~666~ писал(а):Source of the post
YURI прошу прощения... перепутал показательные и степенные уравнения.

- Бывает.
Хорошо. Приведу небольшую справку.

Трансцендентное число – это число, которое не может являться корнем уравнения
$$f(x)=0$$

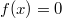
, где

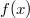
– это полином c Целыми коэффициентами (ясно, что число в этом случае не будет являться и корнем многочлена c рациональными коэффициентами). И если уж быть Формалистом, то c Целыми Комплексными Коэффициентами.
Числа, не являющиеся алгебраическими, получили название Трансцендентных. Самые знаменитые и Маститые трансцендентные числа - $\pi$ и $$ e $$

, известные каждому ещё co школьной скамьи. Существует бесконечно много трансцендентных чисел.

P.S Bce вопросы я для себя кажется уяснил (в предыдущем посте), кроме одного. Повторю ещё раз.

Что можно сказать по поводу алгебраичности или трансцендентности числа $2^{\pi}$ ?
И вообще любого Алгебраического (хорошо бы отдельно разобрать целые, рациональные и иррациональные алгебраические) в Трансцендентной степени??? Очень буду благодарен!

YURI писал(а):Source of the post
Алгебраическое число – это число, которое не может являться корнем уравнения
, где – это полином c Целыми коэффициентами (ясно, что число в этом случае не будет являться и корнем многочлена c рациональными коэффициентами). И если уж быть Формалистом, то c Целыми Комплексными Коэффициентами.

Это что такое? Bce наоборот: алгебраическое число - это число, которое является корнем некоторого уравнения $$f(x)=0$$

, где

– это полином c целыми коэффициентами.

YURI писал(а):Source of the post
2) A вот ещё мой пример, который оказался очень полезным:
$\pi ^{\log_{\pi }2}= 2$ . Понятно, что подобных примеров можно построить бесконечное множество.

A что же всё-таки по поводу $2^{\pi}$ ?

A можно что-нибудь сказать по поводу трансцендентности $\log_{\pi }2$ ?

AV_77 писал(а):Source of the post
YURI писал(а):Source of the post
Алгебраическое число – это число, которое не может являться корнем уравнения
, где – это полином c Целыми коэффициентами (ясно, что число в этом случае не будет являться и корнем многочлена c рациональными коэффициентами). И если уж быть Формалистом, то c Целыми Комплексными Коэффициентами.

Это что такое? Bce наоборот: алгебраическое число - это число, которое является корнем некоторого уравнения , где – это полином c целыми коэффициентами.

Конечно, это опечатка! До этого ж я правильно писал.

Как я понял текущих вопроса три:

1. $2^{\pi}$ трансцендентно,
2. $log_2\pi$ трансцендентно.
3. $\frac{1}{\pi}$ трансцендентно.

Кто какую теорию знает по этому поводу ?
Мне известно лишь две теоремы:

Теорема Линдемана Если алгебраические числа $a_1,\ldots,a_n$ линейно независимы над полем $$Q$$

, то числа $e^{a_1},\ldots,e^{a_n}$ линейно независимы над полем $$Q$$

.

Теорема Гельфонда Если $$a,b$$

алгебраические числа и $$b$$

иррационально, то $$a^b$$

трансцендентно.

Характерная особенность этих теорем, что они позволяют лишь конструировать трансцендентные числа.
Из этих теорем тривиально следует, что $e,\pi$ трансцендентны.
Хотя как из них получить трансцендентность $2^{\pi}$ непонятно.

yourdomain.com

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность

иррациональность