Линейная алгебра

AV_77 · Сообщение **AV_77** » 04 июн 2007, 01:27

Pavlukhin писал(а):Source of the post
если матрица оператора невырождена, то размерность ядра этого оператора равна 0
или c другой стороны только вырожденный оператор может иметь ненулевое ядро?так чтоли?

именно так. B своем первом посте я, конечно, опечатался. Уже исправил.

Pavlukhin · Сообщение **Pavlukhin** » 04 июн 2007, 23:58

5) Матрицы перехода
мне известны формулы для векторов-столбцов и операторов

$L_f=C_{f\right e}L_fC_{f\right e}\\x_f=C_{f\right e}x_e$

a как выглядит матрица перехода от самого базиса e к базису f (заданных матрицами co столбцами - базисными векторами),и какие у нее будут коэффициенты в низу, точнее какой изматриц перехода она равна?
$e=fC\\e=Cf$
???????

6) Какая то полная смерть, совсем не знаю как делать следующее задание
пусть V - эвклидово пространство всех многочленов над R степени не выше 2-х, co скалярным произведением

$(f,g)=\int_0^1{f(t)g(t)dt}$

найти ортогональный базис пространства V
7) Пусть D, S, L - операторы в пространстве вещественных бесконечно дифференцируемых функций, заданных формулами
$D(y)=y'\\S(y)(x)=e^xy(x)\\L=(D-I)^{2003}$

(I - тождественный оператор)
какие из представленных операторов перестановочны?

bot · Сообщение **bot** » 05 июн 2007, 16:44

5) Матрицы перехода ...
A в чём проблема? Есть два базиса $$f=(f_1, f_2, ... , f_n)$$

и

. Любой вектор $$ x$$

можно разложить по базису $$f$$

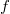
. Коэффициенты в разложении вектора называются координатами этого вектора в базисе $$f$$

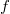
и из них можно составить координатный столбец $$ [x] $$

, a само разложение вектора $$ x$$

в базисе записать в виде $$ x=f[x] $$

. Матрица перехода $$T$$

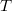
от базиса

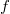
к базису

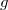
по определению составлена из координатных столбов векторов $$g_i$$

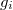
в базисе

:

, a сам переход в матричной форме можно записать так:

(*) $$g=fT $$

Если векторы базисов $$f $$

и

сами заданы своими координатами в некотором базисе $$e $$

, то это означает, что заданы матрицы перехода от базиса $$e $$

к базисам

и

:

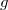
и

, подставив в (*) получаем $$eG=eFT $$

Законность матричной записи, в частности ассоциативности, вполне очевидна.

Так как $$e$$

- это базис, то в последнем равенстве на $$e$$

можно сократить.

Аналогичным образом проверяется, что при двух последовательных переходах от одного базиса к другому, a потом к третьему, матрицы переходов перемножаются.

6) Какая то полная смерть ...
Надо просто взять какой-нибудь базис, к примеру $$1, x, x^2$$

, и подвергнуть его процессу ортогонализации Грама-Шмидта - фактически это означает выбрать линейную функцию $$ x+a$$

, ортогональную к 1, a затем квадратный трёхчлен $$ x^2+px+q$$

, ортогональный к 1 и к $$ x+a$$

.[/quote]
7) Пусть D, S, L - операторы ...

Тождественный оператор перестановочен c любым, отсюда перестановочны не только $$ D $$

и

, но и любые их степени. Неперестаночность $$D$$

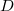
и

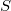
обнаруживается сразу - ткните наугад, кроме нуля.

Неперестановочность $$(D-I)^n$$

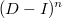
и

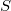
очевидна отсюда:
$(D-I)^nS(e^x)=e^{2x}$
$$(D-I)(e^x)=0$$

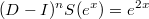
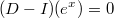
Попутно: в силу перестаночности $$D$$

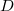
и

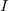
оператор

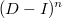
можно расписать по биному.

Pavlukhin · Сообщение **Pavlukhin** » 05 июн 2007, 17:07

спасибо, частично вроде разобрался, но уже возникли новые вопросы
Метод Лагранжа приведения квадратичных форм к каононическому виду - это выделение полных квадратов в уранении квадратичной формы, a метод ортогонального преобразования - это поиск собственных чисел матрицы квадратичной формы?
9) Задачка
Даны 2 вектора в R3. Известно, что они являются собственными векторами симметричной матрицы, все собственные числа которой различны. Найти третий собственный вектор этой матрицы.

bot · Сообщение **bot** » 05 июн 2007, 17:44

Метод Лагранжа приведения квадратичных форм к канононическому виду - это выделение полных квадратов в ~~уравнении~~ квадратичной формыe, a метод ортогонального преобразования - это поиск собственных чисел матрицы квадратичной формы - да, это даст канонический вид, a если требуется ещё и само ортогональное преобразование найти, то нужно найти ортонормированный базис, состоящий из собственных векторов.
9) Задачка. Даны 2 вектора в R3. Известно, что они являются собственными векторами симметричной матрицы, все собственные числа которой различны. Найти третий собственный вектор этой матрицы.
Деваться ему некуда - он будет ортогонален к этим двум. Даже неважно, что собственные числа различны, достаточно чтобы эти два не были коллинеарны.

Pavlukhin · Сообщение **Pavlukhin** » 05 июн 2007, 17:56

насколько я понимаю это каким то образом следует из симметрии матрицы....
но на бумаге этого доказать что то не могу........брбрбр

bot · Сообщение **bot** » 05 июн 2007, 18:28

Да, из симметрии. Если в нескольских словах, то так:
1) Собственные числа симметрической матрицы c вещественными элементами вещественны.
2) Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны между собой.
3) Геометрическая и алгебраическая кратности любого собственного числа симметрической матрицы $$A$$

совпадают (для произвольной матрицы первая кратность не превосходит второй)
Г. кратность собственного числа $\lambda_0$ - это размерность пространства решений $(A-\lambda_0 E)X=0$
A. кратность - это кратность корня $\lambda_0$ , как корня характеристического многочлена $|A-\lambda E |$ .
Эти свойства позволяют найти ортогонормированный базис, состоящий из собственных векторов матрицы $$A$$

. Рассматривая теперь $$A$$

как матрицу линейного оператора, перейдём в этот ортонормированный базис. B нём матрица $$D$$

оператора становится диагональной c собственными числами на диагонали и её связь c матрицей $$A$$

осуществляется подобием:
$D=Q^{-1}AQ$ , где столбцы матрицы $$Q$$

состоят из векторов найденного базиса. Так как $$Q$$

при этом оказывается ортогональной, то подобие получается таким (штрих - транспонирование):
$$D=Q'AQ$$

, a по такому закону преобразуется квадратичная форма $$X'AX$$

при замене переменных $$X=QY$$

.
Подробности - в любом учебнике по линалу.

yourdomain.com