Вопрос по сильной лемме о 4 гомоморфизмах

JeffLebovski

Дана коммутативная диаграмма $$R$$

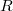
-модулей:
$\xymatrix{A\ar[r]^{\varphi}\ar[d]^{\tau}&B\ar[r]^{\xi}\ar[d]^{\alpha}&C\ar[r]^{\psi}\ar[d]^{\beta}&D\ar[d]^{\nu}\\A'\ar[r]^{\varphi '}&B'\ar[r]^{\eta}&C'\ar[r]^{\psi '}&D'}$
в которой строки- точны, а $\tau$ - эпиморфизм, $\nu$ - мономорфизм. Требуется доказать, что $\operatorname{Im}\alpha=\eta^{-1}(\operatorname{Im}\beta)$ .

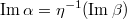
Пусть $b'\in\operatorname{Im}\alpha$ , значит в силу коммутативности $\eta\alpha b=\beta\xi b\Rightarrow \eta b'\subset\operatorname{Im}\beta\Rightarrow b'\in\eta^{-1}\operatorname{Im}\beta$ . А вот обратное вложение доказать не получается. Рассуждал так:
$b'\in\eta^{-1}\operatorname{Im}\beta\Rightarrow\eta b'=\beta c$ . В силу точности в $$C'$$

имеем $\psi '\eta b'=\psi '\beta c=\nu\psi c=0$ , т.к $\nu$ - мономорфизм, то $\psi c=0$ , а в силу точности в $$C$$

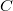
$\eta b'=\eta\alpha b$ , теперь пусть $\alpha b=b''$ , тогда $b'-b''\in\operatorname{Ker}\eta$ , т.е. $\varphi '\tau a=\alpha\varphi a=b'-b''$ , а дальше ступор. Не получается доказать равенство нулю $$b'-b''$$

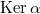
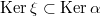
, может ядро какого-нибудь гомоморфизма вкладывается $\operatorname{Ker}\alpha$ ? Пытался доказать, что $\operatorname{Ker}\xi\subset\operatorname{Ker}\alpha$ , но не вышло.

fri739 · Сообщение **fri739** » 15 янв 2012, 19:07

Я начну с места, где ты показал, пользуясь мономорфностью $\nu$ , что $\psi(c)=0$ . Из точности верхней строки теперь следует, что $c=\xi(b)$ для некоторого $b\in B$ . Имеем $\eta(\alpha(b))=\beta(\xi(b))=\beta(c)=\eta(b')$ . Следовательно, $\eta(\alpha(b)-b')=0$ . Точность нижней строки влечет $\alpha(b)-b'=\phi'(a')$ для некоторого $a'\in A'$ . Так как $\tau$ - эпиморфизм, $$a'$$

можно "поднять", то есть существует $a\in A$ такое, что $a'=\tau(a)$ . Теперь имеем

$\displaystyle \alpha(b-\phi(a))=\alpha(b)-\alpha(\phi(a))=\alpha(b)-\phi'(\tau(a))=\alpha(b)-\phi'(a')=\alpha(b)-(\alpha(b)-b')=b'$

Так что $$b'$$

действительно образ относительно $\alpha$ какого элемента из $$B$$

.

JeffLebovski

Во, теперь разобрался, спасибо большое!!!

yourdomain.com