Универсальная диаграмма модулей

JeffLebovski

Доказать, что диаграмма $\{\alpha_t: A_t\to B, t\in T\}$ универсальна относительно данных модулей $$A_t$$

тогда и только тогда, когда:
1)модуль $$B$$

есть объединение подмодулей $\alpha_tA_t$
2)существует такие гомоморфизмы $\pi_t: B\to A_t, t\in T$ , что $\pi_t\alpha_t=\operatorname{id}_{A_t}, \pi_s\alpha_t=0,t\neq s$

fri739 · Сообщение **fri739** » 14 янв 2012, 20:53

Пусть диаграмма $\{\alpha_t: A_t\to B, t\in T\}$ универсальна. По определению это означает, что для любого модуля $$C$$

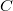
и набора гомоморфизмов $\{\beta_t: A_t\to C, t\in T\}$ существует единственный морфизм $\gamma:B\to C$ такой что для любого $t\in T$ $\gamma\circ \alpha_t=\beta_t$ . Пусть $$t$$

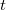
последовательно пробегает все значения множества индексов $$T$$

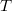
. Для фиксированного $$t$$

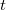
положим

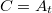
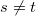
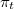
и рассмотрим набор гомоморфизмов $\beta_s=\begin{cases}id_{A_t},s=t\\ 0, s\not=t\end{cases}$ , $s\in T$ . Как было замечено выше, из универсальности следует, что существует единственный гомоморфизм $\pi_t: B\to C=A_t$ такой, что $\pi_t \circ \alpha_t=id_{A_t}$ и $\pi_s \circ \alpha_t=0$ , если $s\not=t$ . Это как раз те $\pi_t$ , которые тебе нужны в п.2.

Пусть теперь диаграмма $\{\alpha_t: A_t\to B, t\in T\}$ обладает свойствами 1 и 2. Покажем, что она универсальна. Для этого возьмем произвольный модуль $$C$$

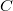
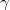
и и набор гомоморфизмов $\{\beta_t: A_t\to C, t\in T\}$ . Нужно построить морфизм $\gamma: B\to C$ со свойствами, указанными выше, и показать, что он такой единственный. Морфизм $\gamma$ строится так: $\gamma=\sum_{t\in T}\beta_t\circ \pi_t$ . Пользуясь свойствами 1 и 2, покажи, что это корректное определение.

JeffLebovski

Кажется я понял. Из 2 следует, что любого $t'\in T$ $\gamma\circ\alpha_{t'}=\sum_{t\in T}\beta_t\circ\pi_t\circ\alpha_{t'}=\beta_t\circ\operatorname{id}_{A_t}=\beta_{t'}.$ . Пусть для некоторого набора $\{\beta_t: A_t\to C, t\in T\}$ существует $\gamma ':B\to C$ , такой что $\gamma '\circ \alpha_t=\beta_t$ . Беру $b\in B=\bigcup\limits_{t\in T}\alpha_t A_t$ , значит существует такое $t\in T$ , что $b\in\alpha_tA_t$ , т.е. $b=\alpha_ta$ , $\gamma 'b=\gamma '\alpha_t a=\beta_t a$ . Теперь $\gamma b=\gamma\alpha_ta=\beta_ta$ . Отсюда следует, что $\gamma=\gamma '$ . Правильно ли я рассуждаю?

fri739 · Сообщение **fri739** » 15 янв 2012, 17:45

JeffLebovski писал(а):Source of the post
Правильно ли я рассуждаю?

В целом верно, но есть недочеты. В первой формуле опечатка. Должно быть так:
для любого $t'\in T$ выполняется $\gamma\circ\alpha_{t'}=\sum_{t\in T}\beta_t\circ\pi_t\circ\alpha_{t'}=\beta_{t'}\circ (\pi_{t'}\circ \alpha_{t'})=\beta_{t'}\circ id_{A_{t'}}=\beta_{t'}$ .

Далее, утверждается, что если $b\in B$ , то $b\in \alpha_t(A_t)$ для некоторого $t\in T$ . Это не совсем так. Произвольный элемент $$b$$

представляется в виде конечной суммы $b=b_{t_1}+\dots+b_{t_n}$ , где $b_{t_i}\in \alpha_{t_i}(A_{t_i})$ .
Дело в том, что в условии 1 на самом деле имеется в виду, что $$B$$

не теоретико-множественное объединение модулей $\alpha_t(A_t)$ , а их сумма . Действительно, возьмем ненулевые элементы $x\in \alpha_t(A_t)\subset B$ , $y\in \alpha_s(A_s)\subset B$ , где $s\not=t$ . Так как $$B$$

-модуль, то $x+y\in B$ , но $x+y\not\in \alpha_t(A_t), \alpha_s(A_s)$ . Так что $$B$$

помимо объединения множеств $\alpha_t(A_t)$ содержит еще и всевозможные конечные линейные комбинации их элементов. На дальнейший ход решения это, врочем, не сильно повлияет.

yourdomain.com